Llei d'elasticidá de Hooke

En física, la llei d'elasticidá de Hooke o llei de Hooke, orixinalmente formulada pa casos d'estiramientu llonxitudinal, establez que l'allargamientu unitariu qu'esperimenta un material elástico ye direutamente proporcional a encomalo aplicada sobre'l mesmu $F$:

La llei de Hooke: la fuercia ye proporcional a la estensión

$\epsilon ={\frac {\delta }{L}}={\frac {F}{AE}}$

siendo $\delta$ l'allargamientu, $L$ el llargor orixinal, $Y$: módulu de Young, $A$ la seición tresversal de la pieza espurrida. La llei aplicar a materiales elásticos hasta una llende denomada llende d'elasticidá llende elásticu.

Esta llei recibe'l so nome del físicu inglés Robert Hooke, contemporaneu d'Isaac Newton, y contribuyente prolíficu de l'arquiteutura. Esta llei entiende numberoses disciplines, siendo utilizada n'inxeniería y construcción, según na ciencia de los materiales. Ante la medrana de que daquién s'apoderara del so descubrimientu, Hooke publicar en forma d'un famosu anagrama, ceiiinosssttuv, revelando'l so conteníu un par d'años más tarde. L'anagrama significa Ut tensio sic vis ("como la estensión, asina la fuercia").

Llei de Hooke pa los resortes

La llei de Hooke describe cuántu allargará un resorte so una cierta fuercia.

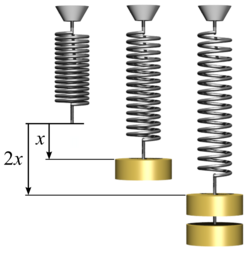
La forma más común de representar matemáticamente la Llei de Hooke ye por aciu la ecuación del muelle o resorte, onde se rellaciona la fuercia $F$ exercida pol resorte cola elongación o allargamientu $\delta$ provocáu pola fuercia esterna aplicada al estremu del mesmu:

$F=-k\delta \,$

onde $k$ llámase constante elástica del resorte y $\delta$ ye'l so elongación o variación qu'esperimenta'l so llargor.

La enerxía de deformación o enerxía potencial elástica $O_{k}$ asociada al estiramientu del resorte vien dada pola siguiente ecuación:

$O_{k}={\frac {1}{2}}k{\delta }^{2}$

Ye importante notar que la $k$ antes definida depende del llargor del muelle y de la so constitución. Vamos Definir agora una constante intrínseca del resorte independiente del llargor d'este y vamos establecer asina la llei diferencial constitutiva d'un muelle. Multiplicando $k$ pol llargor total, y llamando al productu $k_{i}$ o $k$ intrínseca, tiense:

$k={\frac {k_{i}}{L}}$

Vamos Llamar $F(x)$ a la tensión nuna seición del muelle asitiada una distancia x d'unu de los sos estremos el cual vamos tomar como orixe de coordenaes, $k_{\Delta x}$ a la constante d'un pequeñu cachu de muelle de llargor $\Delta x$ a la mesma distancia y $\delta _{\Delta x}$ al allargamientu d'esi pequeñu cachu en virtú de l'aplicación de la fuercia $F(x)$. Pola llei del muelle completu:

$F(x)=-k_{\Delta x}\delta _{\Delta x}=-k_{i}{\frac {\delta _{\Delta x}}{\Delta x}}$

Tomando la llende:

$F(x)=-k_{i}{\frac {{\delta }_{dx}}{dx}}$

que pol principiu de superposición resulta:

$F\left(x\right)=-k_{i}{\frac {d{\delta }}{dx}}=-AE{\frac {d\delta }{dx}}$

Que ye la ecuación diferencial del muelle. Si integrar pa tou $x$, llógrase como ecuación d'onda unidimensional que describe los fenómenos ondulatorios (Ver: Muelle elásticu). La velocidá d'espardimientu de les vibraciones nun resorte calcúlase como:

$c={\sqrt {\frac {Y}{\rho }}}$

Llei de Hooke en sólidos elásticos

La llei de Hooke pa sólidos elásticos xeneraliza la llei de Hooke pa resortes. Na mecánica de sólidos deformables elásticos la distribución de tensiones ye muncho más complicada que nun resorte o una barra espurrida solo según la so exa. La deformación nel casu más xeneral precisa ser descrita por aciu un tensor de deformaciones ente que los esfuercios internos nel material precisen ser representaos por un tensor de tensiones. Estos dos tensores tán rellacionaos por ecuaciones lliniales conocíes por ecuaciones de Hooke xeneralizaes o ecuaciones de Lamé-Hooke, que son les ecuaciones constitutives que caractericen el comportamientu d'un sólidu elásticu llinial. Estes ecuaciones tienen la forma xeneral:

$\sigma _{ij}=\sum _{k,l}C_{ijkl}\varepsilon _{kl}\,$

Gran parte de les estructures d'inxeniería son diseñaes pa sufrir deformaciones pequeñes,arréyense solo na recta de la diagrama d'esfuerciu y deformación.

De tala forma que la deformación $\epsilon$ ye una cantidá adimensional, el módulu $Y$ espresar nes mesmes unidaes que l'esfuerciu $\sigma$ (unidaes pa, psi y ksi). El máximu valor del esfuerciu pal que puede emplegase la llei de Hooke nun material ye conocíu como llende de proporcionalidad d'un material. Nesti casu, los materiales dúctiles que tienen un puntu de cedencia definíu; en ciertos materiales nun puede definise la proporcionalidad de cedencia fácilmente, yá que ye difícil determinar con precisión el valor del esfuerciu $\sigma$ pal que la semeyanza ente $\sigma$ y $\epsilon$ dexe de ser llinial. Al utilizar la llei de Hooke en valores mayores que la llende de proporcionalidad nun va conducir a nengún error significativu. En resistencia de materiales arreyar nes propiedaes físiques de materiales, como resistencia, ductibilidad y resistencia d'escomiu; que pueden afectase por cuenta de la aleación, el tratamientu térmicu y el procesu de manofactura.

Casu unidimensional

Nel casu d'un problema unidimensional onde les deformaciones o tensiones en direiciones perpendiculares a una direición dada son irrelevantes o pueden inorase $\sigma =\sigma _{11}$, $\epsilon =\epsilon _{11}$, $C_{11}=Y$ y la ecuación anterior amenorgar a:

$\sigma =Y\epsilon \,$

onde $Y$ ye'l módulu de Young.

Casu tridimensional isótropo

Pa carauterizar el comportamientu d'un sólidu elásticu llinial y isótropo ríquense amás del módulu de Young otra constante elástica, llamada coeficiente de Poisson ($\nu$). Per otru llau, les ecuaciones de Lamé-Hooke pa un sólidu elásticu llinial y isótropo pueden ser deducíes del teorema de Rivlin-Ericksen, que pueden escribise na forma:

$\epsilon _{xx}={\frac {1}{Y}}\left(\sigma _{xx}-\nu (\sigma _{yy}+\sigma _{zz})\right)\qquad \epsilon _{xy}={\frac {(1+\nu )}{Y}}\sigma _{xy}$

$\epsilon _{yy}={\frac {1}{Y}}\left(\sigma _{yy}-\nu (\sigma _{xx}+\sigma _{zz})\right)\qquad \epsilon _{yz}={\frac {(1+\nu )}{Y}}\sigma _{yz}$

$\epsilon _{zz}={\frac {1}{Y}}\left(\sigma _{zz}-\nu (\sigma _{xx}+\sigma _{yy})\right)\qquad \epsilon _{xz}={\frac {(1+\nu )}{Y}}\sigma _{xz}$

En forma matricial, en términos del módulu de Young y el coeficiente de Poisson como:

${\begin{pmatrix}\varepsilon _{xx}\\\varepsilon _{yy}\\\varepsilon _{zz}\\\varepsilon _{xy}\\\varepsilon _{xz}\\\varepsilon _{yz}\end{pmatrix}}={\begin{pmatrix}{\frac {1}{Y}}&-{\frac {\nu }{Y}}&-{\frac {\nu }{Y}}&&&\\-{\frac {\nu }{Y}}&{\frac {1}{Y}}&-{\frac {\nu }{Y}}&&&\\-{\frac {\nu }{Y}}&-{\frac {\nu }{Y}}&{\frac {1}{Y}}\\&&&{\frac {(1+\nu )}{Y}}&0&0\\&&&0&{\frac {(1+\nu )}{Y}}&0\\&&&0&0&{\frac {(1+\nu )}{Y}}\\\end{pmatrix}}{\begin{pmatrix}\sigma _{xx}\\\sigma _{yy}\\\sigma _{zz}\\\sigma _{xy}\\\sigma _{xz}\\\sigma _{yz}\end{pmatrix}}$

Les rellaciones inverses vienen daes por:

${\begin{pmatrix}\sigma _{xx}\\\sigma _{yy}\\\sigma _{zz}\\\sigma _{xy}\\\sigma _{xz}\\\sigma _{yz}\end{pmatrix}}={\frac {Y}{1+\nu }}{\begin{pmatrix}{\frac {1-\nu }{1-2\nu }}&{\frac {\nu }{1-2\nu }}&{\frac {\nu }{1-2\nu }}&&&\\{\frac {\nu }{1-2\nu }}&{\frac {1-\nu }{1-2\nu }}&{\frac {\nu }{1-2\nu }}&&&\\{\frac {\nu }{1-2\nu }}&{\frac {\nu }{1-2\nu }}&{\frac {1-\nu }{1-2\nu }}&&&\\&&&1&0&0\\&&&0&1&0\\&&&0&0&1\\\end{pmatrix}}{\begin{pmatrix}\varepsilon _{xx}\\\varepsilon _{yy}\\\varepsilon _{zz}\\\varepsilon _{xy}\\\varepsilon _{xz}\\\varepsilon _{yz}\end{pmatrix}}$

Casu tridimensional ortótropo

El comportamientu elásticu d'un material ortotrópico queda carauterizáu por nueve constantes independientes: 3 módulos d'elasticidá llonxitudinal $(Y_{x},Y_{y},Y_{z})$, 3 módulos de rixidez $(G_{xy},G_{yz},G_{zx})$ y 3 coeficientes de Poisson $(\nu _{xy},\nu _{yx},\nu _{zx})$. De fechu pa un material ortotrópico la rellación ente les componentes del tensor tensión y les componentes del tensor deformación vien dada por:

${\begin{pmatrix}\varepsilon _{xx}\\\varepsilon _{yy}\\\varepsilon _{zz}\\\varepsilon _{xy}\\\varepsilon _{xz}\\\varepsilon _{yz}\end{pmatrix}}={\begin{pmatrix}{\frac {1}{Y_{x}}}&-{\frac {\nu _{yx}}{Y_{y}}}&-{\frac {\nu _{zx}}{Y_{z}}}&&&\\-{\frac {\nu _{xy}}{Y_{x}}}&{\frac {1}{Y_{y}}}&-{\frac {\nu _{zy}}{Y_{z}}}&&&\\-{\frac {\nu _{xz}}{Y_{x}}}&-{\frac {\nu _{yz}}{Y_{y}}}&{\frac {1}{Y_{z}}}\\&&&{\frac {1}{2G_{xy}}}&0&0\\&&&0&{\frac {1}{2G_{xz}}}&0\\&&&0&0&{\frac {1}{2G_{yz}}}\\\end{pmatrix}}{\begin{pmatrix}\sigma _{xx}\\\sigma _{yy}\\\sigma _{zz}\\\sigma _{xy}\\\sigma _{xz}\\\sigma _{yz}\end{pmatrix}}$

Onde:

${\frac {\nu _{yx}}{Y_{y}}}={\frac {\nu _{xy}}{Y_{x}}}\qquad {\frac {\nu _{zx}}{Y_{z}}}={\frac {\nu _{xz}}{Y_{x}}}\qquad {\frac {\nu _{yz}}{Y_{y}}}={\frac {\nu _{zy}}{Y_{z}}}\qquad (*)$

Como puede trate les componentes que gobiernen l'allargamientu y les que gobiernen la distorsión tán desacopladas, lo cual significa que polo xeneral ye posible producir allargamientos en redol a un puntu ensin provocar aburuyes y viceversa. Les ecuaciones inverses que dan les deformaciones en función de les tensiones tomen una forma daqué más complicada:

${\begin{pmatrix}\sigma _{xx}\\\sigma _{yy}\\\sigma _{zz}\\\sigma _{xy}\\\sigma _{xz}\\\sigma _{yz}\end{pmatrix}}={\begin{pmatrix}{\frac {1-\nu _{yz}\nu _{yz}}{Y_{y}Y_{z}\Delta }}&{\frac {\nu _{yx}+\nu _{yz}\nu _{zx}}{Y_{y}Y_{z}\Delta }}&{\frac {\nu _{zx}+\nu _{zy}\nu _{yx}}{Y_{y}Y_{z}\Delta }}&&&\\{\frac {\nu _{xy}+\nu _{xz}\nu _{zy}}{Y_{x}Y_{z}\Delta }}&{\frac {1-\nu _{zx}\nu _{xz}}{Y_{x}Y_{z}\Delta }}&{\frac {\nu _{zy}+\nu _{zx}\nu _{xy}}{Y_{x}Y_{z}\Delta }}&&&\\{\frac {\nu _{xz}+\nu _{xy}\nu _{yz}}{Y_{x}Y_{y}\Delta }}&{\frac {\nu _{yz}+\nu _{yx}\nu _{xz}}{Y_{x}Y_{y}\Delta }}&{\frac {1-\nu _{xy}\nu _{yx}}{Y_{x}Y_{y}\Delta }}\\&&&2G_{xy}&0&0\\&&&0&2G_{xz}&0\\&&&0&0&2G_{yz}\\\end{pmatrix}}{\begin{pmatrix}\varepsilon _{xx}\\\varepsilon _{yy}\\\varepsilon _{zz}\\\varepsilon _{xy}\\\varepsilon _{xz}\\\varepsilon _{yz}\end{pmatrix}}$

Onde:

$\Delta :={\frac {1-\nu _{xy}\nu _{yx}-\nu _{xz}\nu _{zx}-\nu _{yz}\nu _{zy}-2\nu _{xy}\nu _{yz}\nu _{zx}}{Y_{x}Y_{y}Y_{z}}}$

De fechu la matriz anterior, que representa al tensor de rixidez, ye simétrica yá que de les rellaciones (*) se la simetría de l'anterior matriz yá que:

${\frac {\nu _{yx}+\nu _{yz}\nu _{zx}}{Y_{y}Y_{z}\Delta }}={\frac {\nu _{xy}+\nu _{xz}\nu _{zy}}{Y_{x}Y_{z}\Delta }}\qquad {\frac {\nu _{zx}+\nu _{zy}\nu _{yx}}{Y_{y}Y_{z}\Delta }}={\frac {\nu _{xz}+\nu _{xy}\nu _{yz}}{Y_{x}Y_{y}\Delta }}\qquad {\frac {\nu _{zy}+\nu _{zx}\nu _{xy}}{Y_{x}Y_{z}\Delta }}={\frac {\nu _{yz}+\nu _{yx}\nu _{xz}}{Y_{x}Y_{y}\Delta }}$

Un casu particular de materiales ortótropos son los materiales transversalmente isótropos lliniales nos que solo fai falta especificar cinco constantes elástiques: $\scriptstyle Y_{t},Y_{L},G_{t},\nu _{t},\nu _{Lt}$, onde $t$ referir a les direiciones tresversales a la direición que se llama llonxitudinal.

Aplicaciones fora del campu de la inxeniería

• Rebotar: La llei de Hooke utilizar prauticantes de puenting, la cuál indíca-yos cuántu va espurrise la cuerda, al esperimentar la fuercia del so pesu cuando cayen al vaciu.

Ver tamién

• Dinamómetru
• Prueba de tensión
• Constante elástica

Referencies

Bibliografía

• R. J. Atkin & N. Fox: An Introduction to the Theory of Elasticity, ed. Dover, 1980.
• Baker, Joanne (06 de 2013). 50 coses qu'hai que saber sobre física, 1ª, páx. 224. ISBN 978-84-672-5575-1.
• Timoshenko, Stephen; Godier J.N. (1951). McGraw-Hill: .
• Ortiz Berrocal, Luis (1998). McGraw-Hill: , páx. 94-96. ISBN 84-481-2046-9.
• Olivella, X.; Agelet de Saracibar, C. (2000). «3», Edicions UPC: , páx. 71-75. ISBN 978-84-8301-412-7.