Llei de Coulomb

La llei de Coulomb puede espresase como:

Llei de Coulomb
llei física

Llei de Coulomb espresando los signos de cargues de distintu signu, y de cargues del mesmu signu.

La magnitú de caúna de les fuercies llétriques con que interactúan dos cargues puntuales en reposu ye direutamente proporcional al productu de la magnitú de dambes cargues ya inversamente proporcional al cuadráu de la distancia que les dixebra y tien la direición de la llinia que les xune. La fuercia ye de repulsión si les cargues son d'igual signu, y d'atraición si son de signu contrariu.

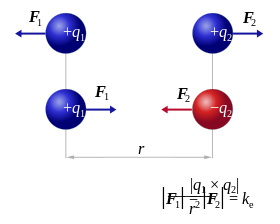
La constante de proporcionalidad depende de la constante dieléctrica del mediu nel que s'atopen les cargues.

Nomar en reconocencia del físicu francés Charles-Augustin de Coulomb (1736-1806), que la enunció en 1785 y forma la base de la electroestática.

Desenvolvimientu de la llei

Charles-Augustin de Coulomb desenvolvió la balanza de torsión cola que determinó les propiedaes de la fuercia electrostática. Esti preséu consiste nuna barra que cuelga d'una fibra capaz de torcese. Si la barra xira, la fibra tiende a faela tornar a la so posición orixinal, colo que conociendo la fuercia de torsión que la fibra exerz sobre la barra, puede determinase la fuercia exercida nun puntu de la barra. La llei de Coulomb tamién conocida como llei de cargues tien que ver coles cargues llétriques d'un material, esto ye, depende de si les sos cargues son negatives o positives.

Variación de la fuercia de Coulomb ente dos cargues puntuales en función de la distancia.

Na barra de la balanza, Coulomb asitió una pequeña esfera cargada y de siguío, a distintes distancies, asitió otra esfera tamién cargada. Depués midió la fuercia ente elles reparando l'ángulu que xiraba la barra.

Diches midíes dexaron determinar que:

• La fuercia d'interacción ente dos cargues $q_{1}\,\!$ y $q_{2}\,\!$ dobla la so magnitú si dalguna de les cargues dobla'l so valor, triplicar si dalguna de les cargues aumenta'l so valor nun factor de trés, y asina socesivamente. Concluyó entós que'l valor de la fuercia yera proporcional al productu de les cargues:

$F\,\!$ $\propto \,\!$ $q_{1}\,\!$     y     $F\,\!$ $\propto \,\!$ $q_{2}\,\!$

en consecuencia:

$F\,\!$ $\propto \,\!$ $q_{1}q_{2}\,\!$

• Si la distancia ente les cargues ye $r\,\!$, al doblala, la fuercia d'interacción mengua nun factor de 4 (2²); al triplicala, mengua nun factor de 9 (3²) y al cuadriplicar $r\,\!$, la fuercia ente cargues mengua nun factor de 16 (4²). Arriendes d'ello, la fuercia d'interacción ente dos cargues puntuales, ye inversamente proporcional al cuadráu de la distancia:

$F\,\!$ $\propto \,\!$ $1 \over r^{2}\,\!$

Acomuñando dambes rellaciones:

$F\,\!$ $\propto \,\!$ $q_{1}q_{2} \over r^{2}\,\!$

Finalmente, introduzse una constante de proporcionalidad pa tresformar la rellación anterior nuna igualdá:

$F=\kappa {\frac {q_{1}q_{2}}{r^{2}}}\,\!$

onde pal sistema internacional d'unidaes:

$\kappa =9\times 10^{9}{\frac {N\cdot m^{2}}{C^{2}}}$

$q_{1}$ y $q_{2}$ son el valor de les cargues en Coulombs (C)

$r$ ye la distancia que dixebra a les cargues en metros (m)

$F$ ye la fuercia d'atraición o repulsión en Newtons (N) (cargues del mesmu signu se repelen, cargues de signu opuestu atráense)

Enunciáu de la llei

La llei de Coulomb ye válida solo en condiciones estacionaries, esto ye, cuando nun hai movimientu de les cargues o, como aproximamientu cuando'l movimientu realizar a velocidaes baxes y en trayectories rectillinies uniformes. Ye por ello que ye llamada fuercia electrostática.

En términos matemáticos, la magnitú $F\,\!$ de la fuercia que caúna de los dos cargues puntuales $q_{1}\,\!$ y $q_{2}\,\!$ exerz sobre la otra separaes por una distancia $d\,\!$ esprésase como:

$F=\kappa {\frac {\left|q_{1}q_{2}\right|}{d^{2}}}\,$

Daes dos cargues puntuales $q_{1}\,\!$ y $q_{2}\,\!$ dixebraes una distancia $d\,\!$ nel vacíu, atráense o repelen ente sigo con una fuercia que la so magnitú ta dada por:

$F=\kappa {\frac {q_{1}q_{2}}{d^{2}}}\,$

La Llei de Coulomb esprésase meyor con magnitúes vectoriales:

$\mathbf {F} _{12}={\frac {1}{4\pi \varepsilon }}{\frac {q_{1}q_{2}}{d^{2}}}\mathbf {o} _{d}={\frac {1}{4\pi \varepsilon }}{\frac {q_{1}q_{2}\mathbf {r} _{12}}{\|\mathbf {r} _{12}\|^{3}}}\,$

onde $\mathbf {o} _{d}$ ye un vector unitariu (que va de la carga 1 a la carga 2), siendo la so direición dende la cargues que produz la fuercia escontra la carga que la esperimenta; $\mathbf {r} _{12}$ ye'l vector de separación ente les cargues. Al aplicar esta fórmula nun exerciciu, tien d'asitiase'l signu de les cargues $q_{1}$ o $q_{2}$, según sían estes positives o negatives.

L'esponente de la distancia, de la llei de Coulomb ye, hasta onde se sabe anguaño, esautamente 2. Esperimentalmente sábese que, si l'esponente fora de la forma $(2+\delta )\,\!$, entós $\left|\delta \right|<10^{-16}\,\!$.

Representación gráfica de la Llei de Coulomb pa dos cargues del mesmu signu.

Reparar qu'esto satisfai la tercera de la llei de Newton por cuenta de qu'implica que fuercies d'igual magnitú actúen sobre $\scriptstyle q_{1}$ y $\scriptstyle q_{2}$. La llei de Coulomb ye una ecuación vectorial ya inclúi el fechu de que la fuercia actúa a lo llargo de la llinia d'unión ente les cargues.

Constante de Coulomb

Artículu principal: Constante de Coulomb

La constante $\kappa \,\!$ ye la Constante de Coulomb y el so valor pa unidaes SI ye $\scriptstyle 1/(4\pi \varepsilon )\,$ Nm²/C².

De la mesma la constante $\varepsilon =\varepsilon _{r}\varepsilon _{0}\,\!$ onde $\varepsilon _{r}\,\!$ ye la permitividad relativa, $\varepsilon _{r}\geq 1\,\!$, y $\varepsilon _{0}=8,85\times 10^{-12}\,\!$ F/m ye la permitividad del vacíu. Cuando'l mediu qu'arrodia a les cargues nun ye'l vacíu hai que tener en cuenta la constante dieléctrica y la permitividad del material. La ecuación de la llei de Coulomb queda finalmente espresada de la siguiente manera:

$F=\kappa {\frac {\left|q_{1}\right|\left|q_{2}\right|}{r^{2}}}\,\!$

La constante, si les unidaes de les cargues atópase en Coulomb ye la siguiente $\scriptstyle K=9\cdot 10^{9}\mathrm {N\cdot m^{2}/C^{2}}$ y la so resultancia va ser en sistema MKS ($\scriptstyle N/C$). Sicasí, si la unidá de les cargues tán en UES (q), la constante espresar de la siguiente forma $\scriptstyle K=\mathrm {dyn\cdot cm^{2}/ues} ^{2}(q)$ y la so resultancia va tar nes unidaes CGS ($\scriptstyle D/UES(q)$).

Potencial de Coulomb

La llei de Coulomb establez que la presencia d'una carga puntual xeneral induz en tol espaciu l'apaición d'un campu de fuercias qu'aparra según la llei de la inversa del cuadráu. Pa modelizar el campu por cuenta de delles cargues llétriques puntuales estátiques puede usase'l principiu de superposición dada la aditividad de les fuercies sobre una partícula. Sicasí, matemáticamente el manexu d'espresiones vectoriales d'esi tipu puede aportar a complicáu, polo que frecuentemente resulta más senciellu definir un potencial llétricu. Pa ello a una carga puntual $\scriptstyle q_{1}$ asígnase-y una función esguilar o potencial de Coulomb $\scriptstyle \phi _{1}$ tal que la fuercia dao pola llei de Coulomb sía expresable como:

$\mathbf {F} _{12}=q_{2}{\boldsymbol {\nabla }}\phi _{1}$

De la llei de Coulomb deduzse que la función esguilar que satisfai l'anterior ecuación ye:

$\phi _{1}(\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}{\frac {q_{1}}{\|\mathbf {r} -\mathbf {r} _{q_{1}}\|}}$

Onde:

$\mathbf {r}$, ye'l vector posición xenéricu d'un puntu onde pretende definise el potencial de Coulomb y $\mathbf {r} _{q_{1}}$, ye'l

vector de posición de la carga llétrica $q_{1}\,$ que'l so campu pretende caracterizase por mediu del potencial.

Llimitaciones de la Llei de Coulomb

• La espresión matemática solo ye aplicable a cargues puntuales estacionaries, y pa casos estáticos más complicaos de carga precisa ser xeneralizada por aciu el potencial llétricu. El campu llétrico creáu por una distribución de carga dada por $\rho$

$\phi (\mathbf {r} )={\frac {1}{4\pi \epsilon }}\int _{V}{\frac {\rho (\mathbf {r} ')}{\|\mathbf {r} -\mathbf {r} '\|}}d^{3}\mathbf {r} '$

• Cuando les cargues llétriques tán en movimientu ye necesariu reemplazar inclusive'l potencial de Coulomb pol potencial vector de Liénard-Wiechert, especialmente si les velocidaes de les partícules son cercanes a la velocidá de la lluz.
• Pa cargues a distancies pequeñes (del orde del tamañu de los átomos), la fuercia electrostática efectiva ten de ser correxida por factores cuánticos. Pa campos bien intensos puede asoceder el fenómenu de la creación bonal de pares de partícula-antipartícula que riquen correxir el campu pa distancies bien curties.

Verificación esperimental de la Llei de Coulomb

Montaxe esperimental pa verificar la llei de Coulomb.

Ye posible verificar la llei de Coulomb por aciu un esperimentu senciellu. Considérense dos pequeñes esferes de masa "m" cargaes con cargues iguales, del mesmu signu, y que cuelguen de dos filos de llargor l, tal como s'indica na figura axunta. Sobre cada esfera actúen trés fuercies: el pesu mg, la tensión de la cuerda T y la fuercia de repulsión llétrica ente les bolines $F_{1}\,\!$. Nel equilibriu:

(1)$T\ \sin \theta _{1}=F_{1}\,\!$

y tamién:

(2)$T\ \cos \theta _{1}=mg\,\!$

Estremando (1) ente (2) miembru a miembru, llógrase:

${\frac {\sin \theta _{1}}{\cos \theta _{1}}}={\frac {F_{1}}{mg}}\Rightarrow F_{1}=mg\tan \theta _{1}$

Siendo $L_{1}\,\!$ la separación d'equilibriu ente les esferes cargaes, la fuercia $F_{1}\,\!$ de repulsión ente elles, vale, acordies cola llei de Coulomb $\scriptstyle F_{1}=q^{2}/(4\pi \varepsilon _{0}L_{1}^{2})$ y, poro, cumplir la siguiente igualdá:

(3)${\frac {q^{2}}{4\pi \varepsilon _{0}L_{1}^{2}}}=mg\tan \theta _{1}\,\!$

Al descargar una de les esferes y ponela, de siguío, en contautu cola esfera cargada, caúna d'elles adquier una carga q/2, nel equilibriu la so separación va ser $L_{2}<L_{1}\,\!$ y la fuercia de repulsíón ente les mesmes va tar dada por:

$F_{2}={\frac {{(q/2)}^{2}}{4\pi \varepsilon _{0}L_{2}^{2}}}={\frac {q^{2}/4}{4\pi \varepsilon _{0}L_{2}^{2}}}\,\!$

Por tar n'equilibriu, tal como se dedució más arriba: $F_{2}=mg.\tan \theta _{2}\,\!$. Y de manera similar llógrase:

(4)${\frac {\frac {q^{2}}{4}}{4\pi \varepsilon _{0}L_{2}^{2}}}=mg.\tan \theta _{2}$

Estremando (3) ente (4), miembru a miembru, llegar a la siguiente igualdá:

(5)${\frac {\left({\cfrac {q^{2}}{4\pi \varepsilon _{0}L_{1}^{2}}}\right)}{\left({\cfrac {q^{2}/4}{4\pi \varepsilon _{0}L_{2}^{2}}}\right)}}={\frac {mg\tan \theta _{1}}{mg\tan \theta _{2}}}\Longrightarrow 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}={\frac {\tan \theta _{1}}{\tan \theta _{2}}}$

Midiendo los ángulos $\theta _{1}\,\!$ y $\theta _{2}\,\!$ y les separaciones ente les cargues $L_{1}\,\!$ y $L_{2}\,\!$ ye posible verificar que la igualdá cumplir dientro del error esperimental. Na práutica, los ángulos pueden resultar difíciles de midir, asina que si'l llargor de los filos que sostienen les esferes son lo suficientemente llargos, los ángulos van resultar lo bastante pequeños como pa faer el siguiente aproximamientu:

$\tan \theta \approx \sin \theta ={\frac {\frac {L}{2}}{l}}={\frac {L}{2l}}\Longrightarrow {\frac {\tan \theta _{1}}{\tan \theta _{2}}}\approx {\frac {\frac {L_{1}}{2l}}{\frac {L_{2}}{2l}}}$

Con esti aproximamientu, la rellación (5) tresformar n'otra muncho más simple:

${\frac {\frac {L_{1}}{2l}}{\frac {L_{2}}{2l}}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Longrightarrow \,\!$ ${\frac {L_{1}}{L_{2}}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Longrightarrow {\frac {L_{1}}{L_{2}}}\approx {\sqrt[{3}]{4}}\,\!$

D'esta forma, la verificación amenorgar a midir la separación ente cargues y comprobar que'l so cociente averar al valor indicáu.

Comparanza ente la Llei de Coulomb y la llei de gravitación universal

Esta comparanza ye relevante una y bones dambes lleis dicten el comportamientu de dos de les fuercies fundamentales de la naturaleza por aciu espresiones matemátiques que la so semeyanza ye bultable.

La llei de la gravitación universal establez que la fuercia d'atraición ente dos mases ye direutamente proporcional al productu de les mesmes ya inversamente proporcional al cuadráu de la distancia que les dixebra. Espresándolo matemáticamente:

$F=G{\frac {m_{1}m_{2}}{r^{2}}}\,$

Siendo:

$G=6,67\cdot 10^{-11}\ {\text{N}}\cdot {\text{m}}^{2}\cdot {\text{kg}}^{-2}\,$ la constante de gravitación universal, :$m_{1},\ m_{2}\,$ les mases de los cuerpos en cuestión y :$r\,$

la distancia ente los centros de les mases. A pesar del chocante paecíu nes espresiones de dambes lleis atopen dos estremes importantes. La primera ye que nel casu de la gravedá nun se pudieron reparar mases de distintu signu como asocede nel casu de les cargues llétriques, y la fuercia ente mases siempres ye curiosa. La segunda tien que ver colos órdenes de magnitú de la fuercia de gravedá y de la fuercia llétrico. Pa esclarialo vamos analizar como actúen dambes ente un protón y un electrón nel átomu d'hidróxenu. La separación permediu ente l'electrón y el protón ye de 5,3·10^-11 m. La carga del electrón y la del protón valen $y^{-}=-1,6\times 10^{-19}C\,\!$ y $p^{+}=1,6\times 10^{-19}C\,\!$ respeutivamente y les sos mases son $m_{y^{-}}=9,11\times 10^{-31}kg\,\!$ y $m_{p^{+}}=1,67\times 10^{-27}kg\,\!$. Sustituyendo los datos:

$F_{Y}=\kappa {\frac {q_{1}q_{2}}{r^{2}}}=8,99\times 10^{9}{\frac {Nm^{2}}{C^{2}}}{\frac {|-1,6\times 10^{-19}C|\times |1,6\times 10^{-19}C|}{5,3\times 10^{-11}m^{2}}}=8,2\times 10^{-8}N\,\!$

$F_{G}=G{\frac {m_{1}m_{2}}{r^{2}}}=6,67\times 10^{-11}{\frac {Nm^{2}}{kg^{2}}}{\frac {9,11\times 10^{-31}kg\times 1,67\times 10^{-27}kg}{5,3\times 10^{-11}m^{2}}}=3,6\times 10^{-47}N\,\!$.

Al comparar resultancies reparar que la fuercia llétrico ye d'unos 39 órdenes de magnitú cimera a encomalo gravitacional. Lo qu'esto representa pue ser ilustráu por aciu un exemplu bien llamativu. 1 C equival a la carga que pasa en 1 s por cualesquier puntu d'un conductor pol que circula una corriente d'intensidá 1 A constante. En viviendes con tensiones de 220 V_rms, esto equival a un segundu d'una bombilla de 220 W (120 W pa les instalaciones doméstiques de 120 V_rms).

Si fuera posible concentrar la mentada carga en dos puntos con una separación de 1 metru, la fuercia d'interacción sería:

$F_{Y}=\kappa {\frac {q_{1}q_{2}}{r^{2}}}=8,99\times 10^{9}{\frac {{\text{Nm}}^{2}}{{\text{C}}^{2}}}{\frac {1\ {\text{C}}\times 1\ {\text{C}}}{{1\ {\text{m}}}^{2}}}=8,99\times 10^{9}\ {\text{N}}\,\!$

esto ye, 916 millones de quilopondios, o'l pesu d'una masa de casi un millón de tonelaes (un teragramu). Si tales cargues pudieren concentrase de la forma indicada más arriba, alloñar so la influencia d'esta enorme fuercia. Si d'esta hipotética disposición de cargues resulten fuercies tan enormes, ¿por qué nun se reparen esplegues dramáticos debíos a les fuercies llétriques? La respuesta xeneral ye que nun puntu dau de cualquier conductor nunca hai demasiáu alloñamientu de la neutralidá llétrica. La naturaleza nunca atropa un Coulomb de carga nun puntu.

Ver tamién

• Carga llétrica
• Campu llétrico
• Lletricidá

Referencies

Bibliografía

• Coulomb, Charles Augustin (1788). Imprimerie Royale: Histoire de l'Académie Royale des Sciences.
• Griffiths, David J. (1998). Prentice Hall: Introduction to Electrodynamics. ISBN 0-13-805326-X.
• Tipler, Paul A.; Mosca, Gene (2008) W. H. Freeman and Company: Physics for Scientists and Engineers. ISBN 0-7167-8964-7.
• Young, Hugh D.; Freedman, Roger A. (2010) Addison-Wesley (Pearson): Sears and Zemansky's University Physics : With Modern Physics. ISBN 978-0-321-69686-1.