Triángulu de Reuleaux

El triángulu Reuleaux ye l'exemplu más senciellu de los llamaos polígonos de Reuleaux, denominaos asina pol científicu y inxenieru que los desenvolvió, Franz Reuleaux. Estos polígonos tienen la particularidá de ser curves d'anchor constante, esto ye, que la distancia ente dos rectes tanxentes paraleles opuestes ye la mesma, independientemente de la direición d'eses rectes. Esto puede apreciase na figura axunta, na que siempres hai cuatro puntox de tangencia col cuadráu, unu en cada llau.

El triángulu de Reuleaux, en cualquier orientación, siempres ye tanxente a un cuadráu.

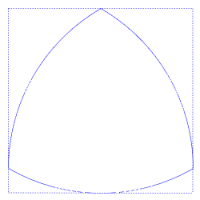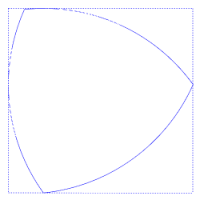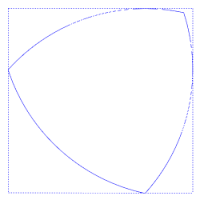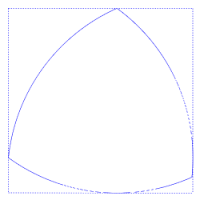
L'área del triángulu de Reuleaux ye ${1 \over 2}(\pi -{\sqrt {3}})a^{2}=0,70477...\ a^{2}$, onde a ye l'anchor constante. L'área d'un círculu d'igual diámetru ye ${\pi \over 4}a^{2}=0,78539...\ a^{2}$, que ye mayor. Entá más, el teorema de Blaschke-Lebesgue establez que'l triángulu de Reuleaux tien menor superficie que cualesquier otra figura d'igual anchor constante.

El so perímetru ye $\pi a$ (vease la esplicación na seición siguiente).

El triángulu de Reuleaux puede xeneralizase a otros polígonos regulares con un númberu impar de llaos, como pue ser el casu de les monedes britániques de 20 peniques (basaes nun heptágonu).

El triángulu de Reuleaux ye una curva d'anchor constante basada nun triángulu equilláteru. La distancia ente cualquier puntu d'una de les curves y el vértiz opuestu ye la mesma.

Trazáu del triángulu de Reuleaux

Partiendo d'un triángulu equilláteru de llau a delíniese, faciendo centru n'unu de los vértices del triángulu y con radiu a, un arcu de circunferencies qu'una ente sigo a los dos vértices restantes, repitir la operación pa cada vértiz y yá se llograría'l triángulu de Reuleaux buscáu. Borrando'l triángulu inicial, l'espaciu central que delimitan de mancomún los trés cirunferencias ye'l triángulu de Reuleaux, una curva d'anchor constante.

Cada unu de los ángulos d'un triángulu equilláteru ye de ${\pi \over 3}$ radianes. Cada unu de los trés arcos ye de llargor ${\pi \over 3}a$. Por tanto'l perímetru del triángulu de Reuleaux ye $\pi a$.

Otros usos

Broca de Harry Watts, basada nel triángulu de Reuleaux.

• Por cuenta de que tolos sos diámetros tienen el mesmu llargor, el triángulu Reuleaux, xunto colos demás polígonos regulares de Reuleaux, ye la respuesta a la entruga "Amás d'un círculu, ¿qué otra forma puede tener una tapa d'alcantariella por que nun caya al traviés del furacu?"
• El rotor d'un Motor Wankel puede fácilmente ser confundíu con un triángulu de Reuleaux. Anque se paez enforma nel so aspeutu, el rotor Wankel tien ente vértices una curva daqué más plana que la del triángulu de Reuleux y por ello nun tien anchu constante.
• En 1914 l'inxenieru británicu Harry James Watts patentó (US-Patent 1241175 y siguientes) una broca (llamada de Harry Watts nos países de fala inglesa) con forma de triángulu de Reuleaux. Esta broca va montada nun dispositivu especial que fai que xire un tanto excéntricamente y asina puede taladrar un furacu con una forma casi esautamente cuadrada. Na figura puede vese la rotación d'esta broca dientro d'un furacu cuadráu. Vese que solo nes esquines dicha broca dexa cuatro pequeñes árees ensin cubrir, que suman un 1,33% del área del cuadráu.

Rodiellos con seición circular y de triángulu de Reuleaux. Deutsche Technikmuseum, Berlín.

• Un triángulu de Reuleaux puede rodar fácilmente, pero nun funcionar bien como rueda por cuenta de que nun tien un centru fixu de rotación. Sicasí, na figura axunta la tabla puede faese avanzar de manera perfctamente horizontal. Nel rodiellu de la esquierda va haber una exa que solo se mueva horizontalmente, ente que na seición del rodiellu de la derecha, que ye un triángulu de Reuleux, tolos puntos tienen daqué de movimientu vertical, como s'aprecia na animación de la broca de Harry Watts.
• La esistencia de los polígonos de Reuleaux ye una bona demostración de que'l qu'una figura tenga anchor constante nun implica que sía un círculu.
• Munchos llapiceros son fabricaos con esti perfil, en llugar de los muncho más tradicionales de seición redonda o hexagonal. Polo xeneral son promocionaos como más cómodos y producen un agarre fayadizu, amás de ser menos probable que rueden fuera les meses.

Versión en tres dimensiones

La interseición d'esferes de radio s centraes nos vértices de tetraedros regulares con llau tamién s ye denomináu'l tetraedru Reuleaux, pero nesti casu nun ye una superficie d'anchor constante. Puede, sicasí, ser realizada dientro d'una superficie d'anchor constante, conocida como'l tetraedru Meissner, reemplazando les sos llendes en forma d'arcu por "parches" de superficie curvada. Alternativamente, la superficie d'un triángulu de Reuleaux en revolución sobre unu de les sos exes simétriques forma una superficie d'anchor constante.

Ver tamién

• Tetraedru de Reuleaux.
• Superelipse

Enllaces esternos

• Shapes of constant width (cut-the-knot)
• Mould, Steve. Numberphile. Brady Haran.
• Weisstein, Eric W. «Reuleaux Triangle» (inglés). MathWorld. Wolfram Research.