Distribución t de Student
En probabilidá y estadística, la distribución t (de Student) ye una distribución de probabilidá que surde del problema d'envalorar la media d'una población de normal distribuyida cuando'l tamañu de la muestra ye pequeñu.
| Distribución t de Student | ||
|---|---|---|
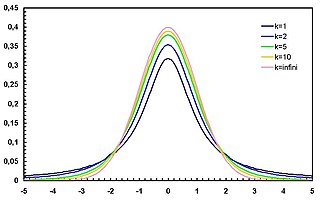 Función de densidá de probabilidá | ||
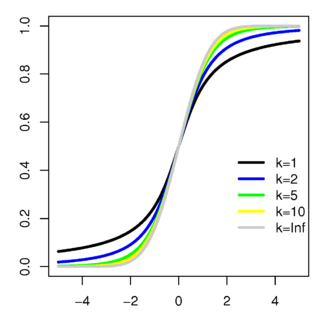 Función de distribución de probabilidá | ||
| Parámetros | graos de llibertá (real) | |
| Función de densidá (pdf) | ||
| Función de distribución (cdf) | onde ye la función hipergeométrica | |
| Media | pa , indefinida pa otros valores mediana = | |
| Moda | ||
| Varianza | pa , indefinida pa otros valores | |
| Coeficiente de simetría | pa | |
| Curtosis | pa | |
| Entropía |
| |
| Función xeneradora de momentos (mgf) | (Non definida) | |
| [editar datos en Wikidata] | ||
Apaez de manera natural al realizar la prueba t de Student pa la determinación de les diferencies ente dos medies muestrales y pa la construcción del intervalu d'enfotu pa la diferencia ente les medies de dos poblaciones cuando se desconoz la esviación típica d'una población y ésta ten de ser envalorada a partir de los datos d'una muestra.
Carauterización
editarLa distribución t de Student ye la distribución de probabilidá del cociente
onde
- Z ye una variable aleatoria distribuyida según una normal típica (de media nula y varianza 1).
- V ye una variable aleatoria que sigue una distribución χ² con graos de llibertá.
- Z y V son independientes
Si μ ye una constante non nula, el cociente ye una variable aleatoria que sigue la distribución t de Student non central con parámetru de non-centralidad .
Apaición y especificaciones de la distribución t de Student
editarSupongamos que X1,..., Xn son variables aleatories independientes distribuyíes de normal, con media μ y varianza σ2. Sía
la media muestral. Entós
sigue una distribución normal de media 0 y varianza 1.
Sicasí, yá que la esviación estándar non siempres ye conocida de mano, Gosset estudió un cociente rellacionáu,
ye la cuasivarianza muestral y demostró que la función de densidá de T ye
onde ye igual a n − 1.
La distribución de T llámase agora la distribución-t de Student.
El parámetru representa'l númberu de graos de llibertá. La distribución depende de , pero non de o , lo cual ye bien importante na práutica.
Intervalos d'enfotu derivaos de la distribución t de Student
editarEl procedimientu pal cálculu del intervalu d'enfotu basáu na t de Student consiste n'envalorar la esviación típica de los datos S y calcular l'error estándar de la media: , siendo entós l'intervalu d'enfotu pa la media: .
Ye esta resultancia'l que s'utiliza nel test de Student: yá que la diferencia de les medies de muestres de dos distribuciones normales distribúyese tamién de normal, la distribución t puede usase pa esaminar si esa diferencia puede razonablemente suponese igual a cero.
Pa efeutos práuticos el valor esperáu y la varianza son:
y pa
Historia
editarLa distribución de Student foi descrita en 1908 por William Sealy Gosset. Gosset trabayaba nuna fábrica de cerveza, Guinness, que prohibía a los sos emplegaos la publicación d'artículos científicos por cuenta de un espardimientu previu de secretos industriales. D'ende que Gosset publicara les sos resultaos sol seudónimu de Student.[1]
Distribución t de Student non estandarizada
editarLa distribución t puede xeneralizase a 3 parámetros, introduciendo un parámero locacional y otru d'escala . La resultancia ye una distribución t de Student non estandarizada que la so densidá ta definida por:[2]
Equivalentemente, puede escribise en términos de (correspondiente a la varianza en cuenta de a la esviación estándar):
Otres propiedaes d'esta versión de la distribución t son:[2]
Referencies
editarEnllaces esternos
editar- Tabla de distribución de T de Student
- Prueba t de Student na UPTC de Colombia (enllaz rotu disponible n'Internet Archive; ver l'historial y la última versión).
- Tabla distribución t de Student
- Distribución t-Student: Puntos porcentuales pa probabilidá cimera
- Probability, Statistics and Estimation n'inglés. Primeros Studentes na páxina 112.
- [1] Calcular la probabilidá d'una distribución t-Student con R (llinguaxe de programación)


![{\displaystyle {\begin{matrix}{\frac {1}{2}}+x\Gamma \left({\frac {\nu +1}{2}}\right)\cdot \\[0.5em]{\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2}};-{\frac {x^{2}}{\nu }}\right)}{{\sqrt {\pi \nu }}\,\Gamma \left({\frac {\nu }{2}}\right)}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02732e546784af1fb16d0dc1bb65dd743e2284ad)








![{\displaystyle {\begin{matrix}{\frac {\nu +1}{2}}\left[\psi ({\frac {1+\nu }{2}})-\psi ({\frac {\nu }{2}})\right]\\[0.5em]+\log {\left[{\sqrt {\nu }}B({\frac {\nu }{2}},{\frac {1}{2}})\right]}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10a24f6de51905e2cbc5b0d4cdae5b1fa7049352)

