Distribución binómica
Esti artículu o seición necesita referencies qu'apaezan nuna publicación acreitada, como revistes especializaes, monografíes, prensa diaria o páxines d'Internet fiables. |
N'estadística, la distribución binómica ye una distribución de probabilidá discreta que cunta'l númberu d'ésitos nuna secuencia de n ensayos de Bernoulli independientes ente sigo, con una probabilidá fixa p d'escurrimientu del ésitu ente los ensayos. Un esperimentu de Bernoulli carauterízase por ser dicotómicu, esto ye, solu dos resultaos son posibles. A unu d'estos denominar ésitu» y tien una probabilidá d'escurrimientu p y al otru, «fracasu», con una probabilidá q = 1 - p.[2]Na distribución binómica l'anterior esperimentu repítise n vegaes, de forma independiente, y trátase de calcular la probabilidá d'un determináu númberu d'ésitos. Pa n = 1, la binómica conviértese, ello ye que nuna distribución de Bernoulli.
| Distribución binómica | ||
|---|---|---|
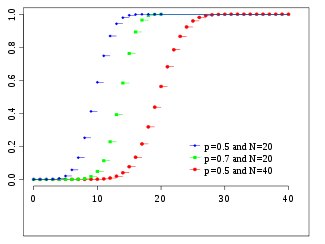 Función de distribución de probabilidá | ||
| Parámetros |
númberu d'ensayos (enteru) probabilidá d'ésitu (real) | |
| Función de probabilidá (fp) | ||
| Función de distribución (cdf) | ||
| Media | ||
| Mediana | Unu de [1] | |
| Moda | ||
| Varianza | ||
| Coeficiente de simetría | ||
| Curtosis | ||
| Entropía | ||
| Función xeneradora de momentos (mgf) | ||
| Función característica | ||
| [editar datos en Wikidata] | ||
Pa representar qu'una variable aleatoria X sigue una distribución binómica de parámetros n y p, escríbese:
La distribución binómica ye la base del test binómicu de significación estadística.
Exemplos
editarLes siguientes situaciones son exemplos d'esperimentos que pueden modelizarse por esta distribución:
- Llánzase un dau diez vegaes y cúntase el númberu X de trés llograos: entós X ~ B(10, 1/6)
Esperimentu binómicu
editarEsisten munches situaciones nes que se presenta una esperiencia binómica. Cada unu de los esperimentos ye independiente de los restantes (la probabilidá de la resultancia d'un esperimentu nun depende de la resultancia del restu). La resultancia de cada esperimentu hai d'almitir namái dos categoríes (a les que se denomina ésitu y fracasu). Les probabilidaes de dambes posibilidaes han de ser constantes en tolos esperimentos (se denotan como p y q o p y 1-p).
Designar por X a la variable que mide'l númberu d'ésitos que se producieron nos n esperimentos.
Cuando se dan estes circunstancies, dizse que la variable X sigue una distribución de probabilidá binómica, y se denota B(n,p).
Carauterístiques analítiques
editarEl so función de probabilidá ye
onde
siendo les combinaciones de en ( elementos tomaos de en )
Exemplu
editarSupongamos que se llanza un dadu (con 6 cares) 51 vegaes y queremos conocer la probabilidá de que'l númberu 3 sala 20 vegaes. Nesti casu tenemos una X ~ B(51, 1/6) y la probabilidá sería P(X=20):
Propiedaes
editarDemostración: Por definición, , pa el primer términu de la suma sume y llogramos , depués recordemos que , pa .
Sustituyendo lo anterior na espresión de , tenemos que . Note que nesti pasu, les atayáronse y el factor " " sale de la suma por ser constante, finalmente pola fórmula de Newton (Teorema del binomiu) tenemos que , entós en formular anterior basta con escoyer tenemos que:
sacando una de la suma tenemos:
.
.
Otra forma más senciella ye la siguiente, sabemos que si son variables aleatories entós tenemos qu'una variable aleatoria binómica ye la suma de variables tipu Bernoulli, entós .
Rellaciones con otres variables aleatories
editarSi tiende a infinitu y ye tal que'l productu ente dambos parámetros tiende a , entós la distribución de la variable aleatoria binómica tiende a una distribución de Poisson de parámetru .
A lo último, cumplir que cuando =0.5 y n ye bien grande (usualmente esíxese que ) la distribución binómica puede averase por aciu la distribución normal.
Propiedaes reproductives
editarDaes m variables binómiques independientes de parámetros ni (i = 1,..., m) y , la so suma ye tamién una variable binómica, de parámetros n1+... + nm, y , esto ye,
Ver tamién
editarReferencies
editar- ↑ Hamza, K. (1995). The smallest uniform upper bound on the distance between the mean and the medien of the binomial and Poisson distributions. Statist. Probab. Lett. 23 21–25.
- ↑ Mode, Elmer B. (1990). Elemento de probabilidá y estadística. Reverte, páx. 171. ISBN 9788429150926. Consultáu'l 5 d'avientu de 2017.
Enllaces esternos
editar- Calculadora Distribución binómica
- [1] Cálculu de la probabilidá d'una distribución binómica con R (llinguaxe de programación)













