Distribución de Poisson
En teoría de probabilidá y estadística, la distribución de Poisson ye una distribución de probabilidá discreta qu'espresa, a partir d'una frecuencia d'escurrimientu mediu, la probabilidá de qu'asoceda un determináu númberu d'eventos mientres ciertu periodu de tiempu. Concretamente, especializar na probabilidá d'escurrimientu de sucesos con probabilidaes bien pequeñes, o sucesos "raros".
| Distribución de Poisson | ||
|---|---|---|
= La exa horizontal ye l'índiz x. La función solamente ta definida en valores enteros de k. Les llinies que conecten los puntos son solu guíes pal güeyu y nun indiquen continuidá. Función de densidá de probabilidá | ||
=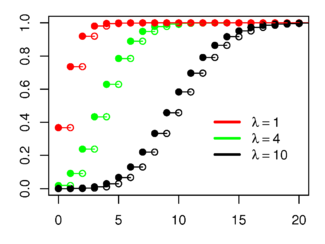 La exa horizontal ye l'índiz k. Función de distribución de probabilidá | ||
| Parámetros | ||
| Función de probabilidá (fp) | ||
| Función de distribución (cdf) | (ónde ye la Función gamma incompleta) | |
| Media | ||
| Mediana | ||
| Moda | ||
| Varianza | ||
| Coeficiente de simetría | ||
| Curtosis | ||
| Entropía | ||
| Función xeneradora de momentos (mgf) | ||
| Función característica | ||
| [editar datos en Wikidata] | ||
Foi afayada por Siméon-Denis Poisson, que la dio a conocer en 1838 nel so trabayu Recherches sur la probabilité des jugements en matières criminelles et matière civile (Investigación sobre la probabilidá de los xuicios en materies criminales y civiles).
Propiedaes
editarLa función de masa o probabilidá de la distribución de Poisson ye
onde
- k ye'l númberu d'escurrimientos del eventu o fenómenu (la función danos la probabilidá de que l'eventu asoceda precisamente k vegaes).
- λ ye un parámetru positivu que representa'l númberu de vegaes que s'espera qu'asoceda'l fenómenu mientres un intervalu dau. Por casu, si'l sucesu estudiáu tien llugar en permediu 4 vegaes per minutu y tamos interesaos na probabilidá de qu'asoceda k vegaes dientro d'un intervalu de 10 minutos, vamos usar un modelu de distribución de Poisson con λ = 10×4 = 40.
- y ye la base de los llogaritmos naturales (y = 2,71828...)
Tanto'l valor esperáu como la varianza d'una variable aleatoria con distribución de Poisson son iguales a λ. Los momentos d'orde cimeru son polinomios de Touchard en λ que los sos coeficientes tienen una interpretación combinatoria. Ello ye que cuando'l valor esperáu de la distribución de Poisson ye 1, entós según la fórmula de Dobinski, el n-ésimo momentu iguala al númberu de particiones de tamañu n.
La moda d'una variable aleatoria de distribución de Poisson con un λ non enteru ye igual a , el mayor de los enteros menores que λ (los símbolos representen la función parte entera). Cuando λ ye un enteru positivu, les modes son λ y λ − 1.
La función xeneradora de momentos de la distribución de Poisson con valor esperáu λ ye
Les variables aleatories de Poisson tienen la propiedá de ser infinitamente divisibles.
La diverxencia Kullback-Leibler dende una variable aleatoria de Poisson de parámetru λ0 a otra de parámetru λ ye
Intervalu d'enfotu
editarUn criteriu fácil y rápido pa calcular un intervalu d'enfotu averáu de λ ye propuestu por Guerriero (2012).[1] Dada una serie d'eventos k (siquier el 15 - 20) nun periodu de tiempu T, les llendes del intervalu d'enfotu pa la frecuencia vienen daes por:
entós les llendes del parámetru tán daes por: .
Rellación con otres distribuciones
editarSumes de variables aleatories de Poisson
editarLa suma de variables aleatories de Poisson independientes ye otra variable aleatoria de Poisson que'l so parámetru ye la suma de los parámetros de les orixinales. Dicho otra manera, si : son N variables aleatories de Poisson independientes, entós : .
Distribución binomial
editarLa distribución de Poisson ye'l casu llende de la distribución binomial. Ello ye que si los parámetros n y d'una distribución binomial tienden a infinitu (nel casu de 'n') y a cero (nel casu de ) de manera que calténgase constante, la distribución llende llograda ye de Poisson.
Aproximamientu normal
editarDe resultes del teorema central de la llende, pa valores grandes de , una variable aleatoria de Poisson X puede averase por otra normal yá que el cociente
converxe a una distribución normal de media 0 y varianza 1.
Distribución esponencial
editarSupóngase que pa cada valor t > 0, que representa'l tiempu, el númberu de sucesos de ciertu fenómenu aleatoriu sigue una distribución de Poisson de parámetru λt. Entós, los tiempos trescurríos ente dos sucesos socesivos sigue la distribución esponencial.
Exemplu
editarSi'l 2% de los llibros enllibraos en ciertu taller tien encuadernación defectuosa, pa llograr la probabilidá de que 5 de 400 llibros enllibraos nesti taller tengan encuadernaciones defectuoses usamos la distribución de Poisson. Nesti casu concretu, k ye 5 y, λ, el valor esperáu de llibros defectuosos ye'l 2% de 400, esto ye, 8. Poro, la probabilidá buscada ye
Procesos de Poisson
editarLa distribución de Poisson aplicar a dellos fenómenos discretos de la naturaleza (esto ye, aquellos fenómenos qu'asoceden 0, 1, 2, 3,... vegaes mientres un periodu definíu de tiempu o nun área determinada) cuando la probabilidá d'escurrimientu del fenómenu ye constante nel tiempu o l'espaciu. Exemplos d'estos eventos que pueden ser modelaos pola distribución de Poisson inclúin:
- El númberu d'autos que pasen al traviés d'un ciertu puntu nuna ruta (abondo distantes de los semáforos) mientres un periodu definíu de tiempu.
- El númberu d'errores d'ortografía qu'unu comete al escribir una única páxina.
- El númberu de llamaes telefóniques nuna central telefónica per minutu.
- El númberu de servidores web aportaos per minutu.
- El númberu d'animales muertos atopaos por unidá de llargor de ruta.
- El númberu de mutaciones de determinada cadena d'ADN dempués de cierta cantidá de radiación.
- El númberu de nucleos atómicos inestables que s'han desintegráu nun determináu periodu.
- El númberu d'estrelles nun determináu volume d'espaciu.
- La distribución de receptores visuales na retina del güeyu humanu.
- El maxín[2] d'un inventor a lo llargo de la so carrera.
- La distribución de la riqueza humana.
Ver tamién
editarReferencies
editar- ↑ Guerriero V.. «Power Law Distribution: Method of Multi-scale Inferential Statistics». J. Mod. Math. Fr. http://www.seipub.org/sjmmf/MostDownloaded.aspx.
- ↑ Invention and Inventivity Is a Random, Poisson Process: A Potential Guide to Analysis of General Creativity http://www.leaonline.com/doi/pdfplus/10.1207/s15326934crj1103_3









![{\displaystyle \lambda [1\!-\!\ln(\lambda )]\!+\!y^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\ln(k!)}{k!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45af52cfc82f1d0b893201704494fc2873b03711)

