Socesión matemática
N'analís matemáticu y álxebra, una socesión ye una aplicación que'l so dominiu ye'l conxuntu de los númberos naturales y el so codominio ye cualesquier otru conxuntu , xeneralmente de númberos de distinta naturaleza, tamién pueden ser figures xeométriques o funciones. Cada unu d'ellos ye denomináu términu (tamién elementu o miembru) de la socesión y al númberu d'elementos ordenaos (posiblemente infinitos) denominar la llargor de la socesión. Nun tien de confundir se con una serie matemática, que ye la suma de los términos d'una socesión.
A diferencia d'un conxuntu, l'orde en qu'apaecen los términos sí ye relevante y un mesmu términu puede apaecer en más d'una posición. De manera formal, una socesión puede definise como una función sobre'l conxuntu de los númberos naturales (o un subconxuntu del mesmu) y ye por tanto una función discreta.
Por casu, la socesión (A, B, C) ye una socesión de lletres que difier de la socesión (C, A, B). Nesti casu falar de socesiones finitas (de llargor igual a 3). Un exemplu de socesión infinita sería la socesión de númberos positivos pares: 2, 4, 6, 8...
N'ocasiones identificar a les socesiones finitas con pallabres sobre un conxuntu. Puede considerase tamién el casu d'una socesión vacida (ensin elementos), pero esti casu puede escluyise dependiendo del contestu.
Historia
editarLes socesiones que siguen una regla determinada llamaron siempres l'atención de los matemáticos de toles xeneraciones. Pero, a pesar d'esto y de que se conocíen dende tiempos alloñaos, nun fueron estudiaes de forma detallada hasta la dómina de mayor desenvolvimientu de les matemátiques nel sieglu XVIII. Foi nesi tiempu cuando se perfeccionó'l conceutu de llende d'una socesión como'l valor al cual avérense de forma socesiva los sos términos.
Ensin cuestión dalguna, Leonhard Euler foi'l matemáticu más destacáu d'esa dómina, gracies a les sos contribuciones decisives en diversos campos de les matemátiques, sobremanera, nel campu de les socesiones y de les series numbériques. Tamién cabo destacar al matemáticu italianu Leonardo de Pisa, quien, nel sieglu sieglu XII, introdució n'Europa una de les socesiones matemátiques que mayor esistencia tien nos fenómenos naturales, los númberos de Fibonacci.
Polo xeneral, les socesiones utilizar pa representar llistes ordenaes d'elemento pero, sobremanera, dientro de les matemátiques discretes son emplegaes d'otres diverses maneres como, por casu, dientro de les ciencies de la computación y na teoría de xuegos.
Xeneralidaes
editarNotación
editarEsisten distintos notaciones y nociones de socesión en matemátiques, dependiendo del área d'estudiu, dalgunes de les cualos (como por casu socesión exacta) nun queden entendíes na notación que s'introduz de siguío.
Suelse usar la notación pa indicar una socesión, onde fai referencia al elementu de la socesión na posición n, llamáu términu xeneral. El subíndice indica'l llugar qu'ocupa en dicha socesión. Un exemplu puede ser el de los númberos positivos pares, denotando dicha socesión por :
entós
Nel casu de que los elementos de la socesión queden determinaos por una regla, puede especificase la socesión faciendo referencia a la fórmula d'un términu arbitrariu. Na socesión anterior puede especificase por aciu la fórmula .
Ye frecuente atopar socesiones onde los subíndices que denoten posición empecipien dende cero, en vegada dende unu, particularmente en matemática discreta o en ciencies de la computación. Tamién puede usase una variable distinta a n pa denotar el términu xeneral, cuando asina convenga pa evitar tracamundiu con otres variables.
Na lliteratura ye posible atopar una gran variedá de notaciones alternatives. Por casu, usu de paréntesis en cuenta de llaves, o indicaciones de les llendes por aciu variantes con super y subíndices, de siguío amuésense dellos pocos exemplos:
Socesiones definíes por recurrencia
editarUna rellación de recurrencia pa una socesión ye una ecuación la cual establez el términu an en función de los términos anteriores pa tolos enteros n tales que . La socesión en sí ye la solución de la rellación de recurrencia si los sos términos cumplen la rellación pa tou enteru positivu n.
Los algoritmos recursivos apurren solución a un problema de tamañu n en términos de la solución d'unu o más casos del mesmu problema, pero de menor tamañu. Un exemplu de socesión per recurrencia ye la socesión de Fibonacci, na cual, cada términu a partir del terceru ye la suma de los dos términos anteriores. Esta socesión en términos xenerales defínese como:
Cuando se realiza la complexidá d'un algoritmu recursivo basáu nuna socesión, llógrase una rellación de recurrencia qu'espresa'l númberu d'operaciones necesaries pa resolver un problema de tamañu n en términos del númberu d'operaciones necesaries pa resolver el mesmu problema con unos datos de tamañu menor.
D'esta manera, puede comprobase la esistencia d'una gran rellación ente les rellaciones de recurrencia y la recursión, yá que sirven pa resolver una gran cantidá de problemes como, por casu, calcular el interés compuestu, calcular el númberu de movimientos del xuegu de les Torres de Hanói y el númberu de coneyos d'una islla (problema propuestu por Fibonacci y rellacionáu, por tanto, cola socesión de Fibonacci).
Exemplos
editarEnte les socesiones comunes y bien utilizaes pueden atopase les que tán en progresión aritmética o en progresión xeométrica. La diferencia básica ye que na socesión aritmética la razón de cambéu ente un miembru y otru ye la suma o resta de la mesma razón, y na socesión xeométrica el siguiente númberu de la socesión llograr por multiplicar o estremar la razón de cambéu. Sía que non la razón de cambéu ye constante y nun puede variar, nun siendo que'l cambéu de la razón tamién correspuenda a una socesión, lo que supón tener una socesión dientro d'otra socesión.
Definición formal y propiedaes básiques
editarLes distintes definiciones suelen tar amestaes al área de trabayu, la más común y xeneral ye la definición de socesión numbérica, na práutica usen socesión de forma intuitiva.
Definición formal
editarUna socesión numbérica formalízase como una aplicación de los númberos naturales sobre otru conxuntu numbéricu X, de manera:
Una socesión siendo'l conxuntu X = N puede ser por casu, la socesión de Fibonacci. Por norma xeneral, la socesión numbérica formalízase como una aplicación de los númberos naturales nos númberos reales. Sía que non se denota a cencielles como o, si dar por entendíu que los subíndices son enteros, tamién se denota como .
El nome que recibe la socesión tamién puede faer referencia a los valores que toma sobre los reales; asina, si la imaxe de fueren los racionales, ye dicir fracciones enteres del tipu , puede llamase socesión de númberos racionales, y lo mesmo pa los irracionales, naturales, enteros, alxebraicos, trascendentes, ...
Finitud y infinitud
editarUna socesión finita (de llargor r) con elementos pertenecientes a un conxuntu S, defínese como una función
.
y nesti casu l'elementu correspuende a . Por casu, la socesión finita, (de llargor 4) de númberos primos menores que 10 (2,3,5,7) correspuende a la función (onde ye'l conxuntu de númberos primos) definida por:
.
Una socesión infinita con elementos pertenecientes a un conxuntu S, defínese como una función
.
onde, de forma análoga, correspuende a .
Subsocesión
editarUna subsocesión o socesión parcial d'una socesión ye la socesión formada de la socesión dada por aciu la eliminación de dalgunos de los sos elementos ensin alteriar la posición relativa de los elementos restantes. Por casu, la socesión formada polos númberos pares positivos (2, 4, 6, ...) ye una socesión parcial de los númberos naturales (1, 2, 3, ...). Les posiciones de dellos elementos camuden cuando s'esanicien otros elementos. Sicasí, les posiciones relatives caltiénense.
Formalmente, una subsocesión d'una socesión ye cualquier socesión de la forma , onde ye una socesión puramente creciente d'enteros positivos. Obviamente pa una socesión esisten delles subsocesiones.[1]
Socesiones monótones
editarNuna socesión monótona, la diferencia ente cada términu y el siguiente ye siempres del mesmu signu. Pueden ser crecientes o decrecientes.[2]
Una socesión creciente ye aquella na que s'impon la desigualdá non estricta , esto ye, na que cada términu ye menor o igual al términu siguiente. Dientro d'estes puédense incluyir, ente otres, les socesiones constantes. Si imponse la condición de que , esto ye, que'l siguiente términu siempres sía puramente mayor que'l so predecesor , denominar socesiones puramente crecientes.
De la mesma manera puede definise la socesión decreciente, según el términu xeneral, si . Va Ser puramente decreciente si .
Socesiones acutaes
editarPueden dase trés formes de socesión acutada:
- Una socesión {an} va tar acutada superiormente nel casu qu'esista un númberu real M que llinde de la siguiente forma la secuencia: {an} ≤ M.
- Per otru llau, la socesión va tar acutada inferiormente cuando un númberu real N la llende de la forma contraria a l'anterior: {an} ≥ N.
- Finalmente, en casu de que se dean dambes opciones {an} va ser una socesión acutada.
Llendes y converxencia
editarSocesiones Converxentes
editarUna propiedá importante de les socesiones ye la converxencia. Si una socesión converxe, esta tiende a un valor particular conocíu como llende. Si una socesión converxe a dalguna llende, entós ye converxente. Una socesión que nun ye converxente ye diverxente.
Informalmente, una socesión tien llende si los elementos de la socesión fáense cada vez más y más cercanos a dalgún valor (llamada llende de la socesión), y quédense «arbitrariamente» cercanos a , lo que significa que dau un númberu real mayor que cero, toos menos un númberu finito d'elementos de la socesión tienen una distancia a menor que .
Formalmente, una socesión , converxe a o tien por llende (cuando ), y escríbese,
cuando,
Si una socesión ye converxente, entós el ye únicu y la socesión ye acutada.
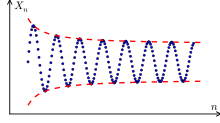
La socesiones trémboles son diverxentes. Los sos términos alternen indefinidamente de mayor a menor o viceversa, polo que nun tienen llende. Intuitivamente llámase socesión alternada cuando alterna valores de signu opuestu, como que xenera la socesión: a0=1, -1, 1, -1, 1, -1, ... utilizada por series alternaes.
Socesiones de Cauchy
editarDada la socesión {an} de númberos reales, llámase socesión de Cauchy o socesión fundamental, nel casu de que satisfaiga'l requisitu siguiente: dau un númberu real r positivu pueda consiguise dos enteros positivos p, q tal que de p > n0 y q > n0 dedúzase que |cp - cq| < r.[3]
Nos númberos reales toa socesión de Cauchy converxe a dalguna llende. Esta particularidá implica un resultáu importante nel analís real que ye la carauterización de Cauchy pa la converxencia de socesiones:
Una socesión de númberos reales ye converxente (nos reales) si y solu si ye de Cauchy.
Estensión a los reales
editarDada una función , vamos llamar estensión nos reales de a una función que los sos valores coinciden nel dominiu de , esto ye, .
Ye incorreutu representar a la estensión nos reales col mesmu nome ( ), pos, tratar d'una asociación totalmente arbitraria y non unívoca que trai tracamundiu y nun tien sentíu pa delles funciones definíes a cachos. Suelse llamar a la estendida por casu o si ye un polinomiu, o o si son funciones trigonométriques, amestando subíndices si fai falta.
La función f puede adquirir propiedaes de la estendida P, si esiste P con diches propiedaes, como llendes al infinitu, monotonía, acotaciones, ente otres.
Xeneralización en distintes árees
editarEstos exemplos pretenden ser una pequeña muestra de la infinidá, puramente dicha, d'usos que tienen diches socesiones en matemátiques.
El trabayu internu nel desenvolvimientu de cada tema en cada área obliga a diversificar la manera de nomar y notar les socesiones, faciéndose frecuente l'usu d'índices, subíndices y superíndices pa salvar la sobrecarga de notación y faeles más legibles y estétiques tocantes a la presentación.
L'espaciu de socesiones finitas complexes
editarPuede tenese una socesión tal que
L'espaciu de socesiones complexes o ℓ2
editarPuede tenese una socesión tal que
L'espaciu de polinómico K[x]
editarUn polinomiu nun ye más qu'una socesión finita tal que representada como .
L'espaciu de les matrices
editarPuede tenese una socesión tal que , onde .
Nun espaciu vectorial topolóxicu
editarPuede tenese una socesión , onde , onde ye una socesión real arbitraria y B un abiertu.
Socesiones funcionales
editarPuede tenese una socesión de funciones continues .
Nel llinguaxe proposicional
editarSía un alfabetu, vamos llamar al conxuntu de socesiones finitas de n elementos de , defínese inductivamente pola socesión de productos cartesianos siguiente:
- asina .
N'homoloxía simplicial
editarEl complexu de cadenes simplicial del complexu simplicial K, nun ye más qu'una determinada socesión de grupos abelianos y morfismos.
Nel llinguaxe de les categoríes
editarSía una categoría, podemos tener una socesión , onde .
Ver tamién
editarReferencies
editarBibliografía
editar- Fernández Novoa, Jesús (1991). Analís Matemáticu I (Tomu 1). Madrid: UNED. ISBN 9788436216684.
- Watson Fulks. "Cálculu avanzáu".
- J. Dieudonné. " Fundamentos d'analís modernu".
- Lages Lima. " Cursu d'analís matemáticu
- Banach. " Cálculu".
- Spivak . "Calculus"
- V.F. Butúzov. " Analís matemáticu"
Enllaces esternos
editar
- Wikimedia Commons tien conteníu multimedia tocante a Socesión.
- Cálculu de la fórmula d'una socesión