Ecuaciones de Maxwell

Les ecuaciones de Maxwell son un conxuntu de cuatro ecuaciones (orixinalmente 20 ecuaciones) que describen por completu los fenómeno electromagnéticos. La gran contribución de James Clerk Maxwell foi axuntar nestes ecuaciones llargos años de resultaos esperimentales, debíos a Coulomb, Gauss, Ampere, Faraday y otros, introduciendo los conceutos de campu y corriente de desplazamientu, y unificando los campos llétricu y magnéticu nun solu conceutu: el campu electromagnéticu.

Ecuaciones de Maxwell
mathematical descriptions of the electromagnetic field (en) y physical theory (en)
ecuación en derivaes parciales y llei física

Los cuatro ecuaciones de Maxwell describen tolos fenómeno electromagnéticos, equí amuésase la inducción magnética per mediu d'una corriente llétrica.

Desarrollu históricu de les ecuaciones de Maxwell

Semeya de Maxwell.

Ver tamién: Electromagnetismu

Dende finales del sieglu XVIII diversos científicos formularon lleis cuantitatives que rellacionaben les interacciones ente los campos llétricos, los campos magnéticos y les corrientes sobre conductores. Ente estes lleis tán la llei de Ampère, la llei de Faraday o la llei de Lenz. Maxwell llograría unificar toes estes lleis nuna descripción coherente del campu electromagnéticu.

Maxwell diose cuenta de que'l caltenimientu de la carga llétrica paecía riquir introducir un términu adicional na llei de Ampère. Ello ye que anguaño considérase qu'unu de los aspeutos más importantes del trabayu de Maxwell nel electromagnetismu ye'l términu qu'introdució en dicha llei: la derivada temporal d'un campu llétricu, conocida como corriente de desplazamientu. El trabayu que Maxwell publicó en 1865, A Dynamical Theory of the Electromagnetic Field, modificaba la versión de la llei de Ampère colo que se predicía la esistencia d'ondes electromagnétiques arrobinándose, dependiendo del mediu material, a la velocidá de la lluz en dichu mediu. D'esta forma Maxwell identificó la lluz como una onda electromagnética, unificando asina la óptica col electromagnetismu.

Quitando'l cambéu a la llei de Ampère, nenguna de les otres ecuaciones yera orixinal. Lo que fizo Maxwell foi reobtener diches ecuaciones a partir de modelos mecánicos ya hidrodinámicos usando'l so modelu de vórtices de llinies de fuercia de Faraday.

En 1884, Oliver Heaviside xunto con Willard Gibbs arrexuntó estes ecuaciones y reformular na notación vectorial actual. Sicasí, ye importante conocer que al faer eso, Heaviside usó derivaes parciales temporales, distintes a les derivaes totales usaes por Maxwell, na ecuación (54). Ello provocó que se perdiera'l términu $v\times B$ qu'apaecía na ecuación posterior del trabayu de Maxwell (númberu 77). Na actualidá, esti términu úsase como complementariu a estes ecuaciones y conozse como fuercia de Lorentz.

La hestoria ye entá confusa, por cuenta de que'l términu ecuaciones de Maxwell úsase tamién pa un conxuntu d'ocho ecuaciones na publicación de Maxwell de 1865, A Dynamical Theory of the Electromagnetic Field, y esti tracamundiu deber a que seis de los ocho ecuaciones son escrites como tres ecuaciones pa cada exa de coordenaes, asina se puede unu confundir al atopar venti ecuaciones con venti incógnites. Los dos tipos d'ecuaciones son cuasi equivalentes, a pesar del términu esaniciáu por Heaviside nes actuales cuatro ecuaciones.

Detalle de les ecuaciones

Llei de Gauss pal campu llétricu

Artículu principal: Llei de Gauss

Fluxu llétrico d'una carga puntual nuna superficie zarrada.

La llei de Gauss esplica la rellación ente'l fluxu del campu llétricu y una superficie zarrada. Defínese como fluxu llétrico ($\Phi _{Y}\,$) a la cantidá de fluyíu llétricu que traviesa una superficie dada. Análogu al fluxu de la mecánica de fluyíos, esti fluyíu llétricu nun tresporta materia, pero ayuda a analizar la cantidá de campu llétricu (${\vec {Y}}$) que pasa por una superficie S. Matemáticamente esprésase como:

$\Phi _{Y}=\oint _{S}{\vec {Y}}\cdot {\rm {{d}{\vec {S}}}}$

La llei diz que'l fluxu del campu llétricu al traviés d'una superficie zarrada ye igual al cociente ente la carga (q) o la suma de les cargues qu'hai nel interior de la superficie y la permitividad llétrica nel vacíu ($\varepsilon _{0}$), asina:

$\oint _{S}{\vec {Y}}\cdot d{\vec {S}}={\frac {q}{\varepsilon _{0}}}$

La forma diferencial de la llei de Gauss, en forma llocal, afirma que pol teorema de Gauss-Ostrogradsky, la diverxencia del campu llétricu ye proporcional a la densidá de carga llétrica, esto ye,

${\vec {\nabla }}\cdot {\vec {Y}}={\frac {\rho }{\varepsilon _{0}}}$

onde $\rho$ ye la densidá de carga nel mediu interior a la superficie zarrada. Intuitivamente significa que'l campu Y diverxi o sale dende una carga ${\frac {\rho }{\varepsilon _{0}}}$, lo que se representa gráficamente como vectores que salen de la fonte que les xenera en toes direiciones. Por convención si'l valor de la espresión ye positivu entós los vectores salen, si ye negativu estos entren a la carga.

Pa casos xenerales tien d'introducise una cantidá llamada densidá de fluxu llétrico (${\vec {D}}$) y la nuesa espresión llogra la forma:

${\vec {\nabla }}\cdot {\vec {D}}=\rho$

Llei de Gauss pal campu magnéticu

Artículos principales: Llei de Gauss y Monopolo magnéticu

Les llinies de campu magnéticu empiecen y terminen nel mesmu llugar, polo que nun esiste un monopolo magnéticu.

Esperimentalmente llegóse al resultáu de que los campos magnéticos, a diferencia de los llétricos, nun empiecen y terminen en cargues distintes. Esta llei primordialmente indica que les línea de los campos magnéticos tienen de ser cerraes. N'otres pallabres, dizse que sobre una superficie zarrada, seya como quier esta, nun vamos ser capaces de zarrar una fonte o sumidoriu de campu, esto espresa la inesistencia del monopolo magnéticu. Al zarrar un dipolo nuna superficie zarrada, nun sale nin entra fluxu magnético, polo tanto'l campu magnéticu nun diverxe, nun sale de la superficie. Entós la diverxencia ye cero. Matemáticamente esto esprésase asina:

${\vec {\nabla }}\cdot {\vec {B}}=0$

onde ${\vec {B}}$ ye la densidá de fluxu magnético, tamién llamada inducción magnética. Ye claro que la diverxencia seya cero porque nun salen nin entren vectores de campu sinón qu'esti fai caminos zarraos. El campu nun diverxe, ye dicir la diverxencia de B ye nula.

La so forma integral equivalente:

$\oint _{S}{\vec {B}}\cdot d{\vec {S}}=0$

Como na forma integral del campu llétricu, esta ecuación solo funciona si la integral ta definida nuna superficie zarrada.

Llei de Faraday-Lenz

Artículu principal: Llei de Faraday

La llei de Faraday fálanos sobre la inducción electromagnética, la qu'anicia una fuercia electromotriz nun campu magnéticu. Ye habitual llamala llei de Faraday-Lenz n'honor a Heinrich Lenz una y bones el signu menos provién de la Llei de Lenz. Tamién se-y llama como llei de Faraday-Henry, por cuenta de que Joseph Henry afayó esta inducción de manera separada a Faraday pero cuasi simultáneamente. Lo primero que se debe introducir ye la fuercia electromotriz (${\mathcal {Y}}$), si tenemos un campu magnéticu variable col tiempu, una fuercia electromotriz ye inducida en cualesquier circuitu llétricu; y esta fuercia ye igual a menos la derivada temporal del fluxu magnético, asina:

${\mathcal {Y}}=-{\frac {d\phi _{B}}{dt}}$, como'l

campu magnéticu ye dependiente de la posición tenemos que'l fluxu magnético ye igual a:

$\phi _{B}=\int _{S}{\vec {B}}\cdot d{\vec {S}}$.

Amás, el qu'esista fuercia electromotriz indica qu'esiste un campu llétricu que se representa como:

${\mathcal {Y}}=\oint {\vec {Y}}\cdot d{\vec {l}}$

colo que finalmente se llogra la espresión de la llei de Faraday:

$\oint {\vec {Y}}\cdot d{\vec {l}}=-\int _{S}{d{\vec {B}} \over dt}\cdot d{\vec {S}}$

Lo qu'indica qu'un campu magnéticu que depende del tiempu implica la esistencia d'un campu llétricu, del que la so circulación per un camín arbitrariu zarráu ye igual a menos la derivada temporal del fluxu magnético en cualquier superficie llindada pel camín zarráu.

El signu negativu esplica que'l sentíu de la corriente inducida ye tal que'l so fluxu oponer a la causa que la produz, compensando asina la variación de fluxu magnético (Llei de Lenz).

La forma diferencial llocal d'esta ecuación ye:

${\vec {\nabla }}\times {\vec {Y}}=-{\frac {\partial {\vec {B}}}{\partial t}}$

Esto ye, el rotacional del campu llétricu ye la derivada de la inducción magnética con respectu al tiempu.

Interprétase como sigue: si esiste una variación de campu magnéticu B entós este provoca un campu llétricu Y o bien la esistencia d'un campu magnéticu non estacionariu nel espaciu llibre provoca circulaciones del vector Y a lo llargo de llinies zarraes. En presencia de cargues llibres, como los electrones, el campu Y puede mover les cargues y producir una corriente llétrica. Esta ecuación rellaciona los campos llétrico y magnético, y tien otres aplicaciones práutiques como los motores llétricos y los xeneradores llétricos y esplica el so funcionamientu. Más precisamente, demuestra qu'un voltaxe puede ser xeneráu variando'l fluxu magnético que traviesa una superficie dada.

Llei de Ampère xeneralizada

Artículu principal: Llei de Ampère xeneralizada

Ampère formuló una rellación pa un campu magnéticu inmóvil y una corriente llétrica que nun varia nel tiempu. La llei de Ampère diznos que la circulación nun campu magnéticu (${\vec {B}}$) a lo llargo d'una curva zarrada C ye igual a la densidá de corriente (${\vec {J}}$) sobre la superficie zarrada na curva C, matemáticamente asina:

$\oint _{C}{\vec {B}}\cdot d{\vec {l}}=\mu _{0}\int _{S}{\vec {J}}\cdot d{\vec {S}}$

onde $\ \mu _{0}$ ye la permeabilidá magnética nel vacíu.

Pero cuando esta rellación considerar con campos que sí varien al traviés del tiempu llega a cálculos erróneos, como'l de violar la caltenimientu de la carga. Maxwell corrixó esta ecuación pa llograr afaela a campos non estacionarios y darréu pudo ser comprobada esperimentalmente por Heinrich Rudolf Hertz.

Maxwell reformuló esta llei asina:

$\oint _{C}{\vec {B}}\cdot d{\vec {l}}=\mu _{0}\int _{S}{\vec {J}}\cdot d{\vec {S}}+\mu _{0}\varepsilon _{0}{\frac {d}{dt}}\int _{S}{\vec {Y}}\cdot d{\vec {S}}$

Nel casu específicu estacionariu esta rellación correspuende a la llei de Ampère, amás confirma qu'un campu llétricu que varia col tiempu produz un campu magnéticu y amás ye consecuente col principiu de caltenimientu de la carga.

En forma diferencial, esta ecuación toma la forma:

${\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {J}}+\mu _{0}\varepsilon _{0}{\frac {\partial {\vec {Y}}}{\partial t}}$

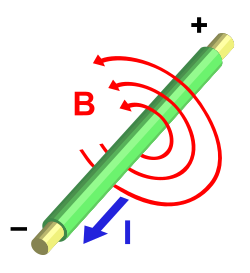
En forma senciella esta ecuación esplica que si se tien un conductor, un alambre rectu que tien una densidá de corriente J, esta provoca l'apaición d'un campu magnéticu B rotacional alredor del alambre y que'l rotor de B apunta nel mesmu sentíu que J.

En medios materiales

Pal casu de que les cargues tean en medios materiales, y asumiendo qu'estos son lliniales, homoxéneos, isótropos y non dispersivos, podemos atopar una rellación ente los vectores intensidá llétrica y inducción magnética al traviés de dos parámetros conocíos como permitividad llétrica y la permeabilidá magnética:

${\vec {D}}=\varepsilon {\vec {Y}}=\varepsilon _{0}\varepsilon _{r}{\vec {Y}}$

${\vec {B}}=\mu {\vec {H}}=\mu _{0}\mu _{r}{\vec {H}}$

Pero estos valores tamién dependen del mediu material, polo que se diz qu'un mediu ye llinial cuando la rellación ente Y/D y B/H ye llinial. Si esta rellación ye llinial, matemáticamente puede dicise que $\varepsilon$ y $\mu$ tán representaes por una matriz 3x3. Si un mediu ye isótropo ye porque esta matriz pudo ser diagonalizada y consecuentemente ye equivalente a una función $\varepsilon (x,y,z)$; si nesta diagonal unu de los elementos ye distintu al otru dizse que ye un mediu anisótropo. Estos elementos tamién son llamaos constantes dieléctriques y, cuando estes constantes nun dependen de la so posición, el mediu ye homoxéneu.

Los valores de $\varepsilon$ y $\mu$ en medios lliniales nun dependen de les intensidaes del campu. Per otru llau, la permitividad y la permeabilidá son esguilares cuando les cargues tán en medios homoxéneos y isótropos. Los medios heteroxéneos y isótropos dependen de les coordenaes de cada puntu polo que los valores, esguilares, van depender de la posición. Los medios anisótropos son tensores. Finalmente, nel vacíu tantu $\ \rho$ como ${\vec {J}}$ son cero porque suponemos que nun hai fontes.

Na siguiente tabla atopamos les ecuaciones como se les fórmula nel casu xeneral y na materia.

Nel vacíu	-----	${\vec {\nabla }}\cdot {\vec {Y}}={\frac {\rho }{\varepsilon _{0}}}$	${\vec {\nabla }}\cdot {\vec {D}}=\rho$
${\vec {\nabla }}\cdot {\vec {B}}=0$	${\vec {\nabla }}\cdot {\vec {B}}=0$
${\vec {\nabla }}\times {\vec {Y}}=-{\frac {\partial {\vec {B}}}{\partial {t}}}$	${\vec {\nabla }}\times {\vec {Y}}=-{\frac {\partial {\vec {B}}}{\partial {t}}}$
${\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {J}}+\mu _{0}\varepsilon _{0}{\frac {\partial {\vec {Y}}}{\partial t}}$	${\vec {\nabla }}\times {\vec {H}}={\vec {J}}+{\frac {\partial {\vec {D}}}{\partial {t}}}$

Ecuaciones de Maxwell

Les ecuaciones de Maxwell como agora conocer son los cuatro citaes enantes y a manera de resume pueden atopase na siguiente tabla:

Nome	Forma diferencial	Forma integral
Llei de Gauss:	${\vec {\nabla }}\cdot {\vec {Y}}={\frac {\rho }{\varepsilon _{0}}}$	$\oint _{S}{\vec {Y}}\cdot d{\vec {s}}={\frac {q}{\varepsilon _{0}}}$
Llei de Gauss pal campu magnéticu:	${\vec {\nabla }}\cdot {\vec {B}}=0$	$\oint _{S}{\vec {B}}\cdot d{\vec {s}}=0$
Llei de Faraday:	${\vec {\nabla }}\times {\vec {Y}}=-{\frac {\partial {\vec {B}}}{\partial t}}$	$\oint _{C}{\vec {Y}}\cdot d{\vec {l}}=-\ {d \over dt}\int _{S}{\vec {B}}\cdot d{\vec {s}}$
Llei de Ampère xeneralizada:	${\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {J}}+\mu _{0}\varepsilon _{0}{\frac {\partial {\vec {Y}}}{\partial t}}$	$\oint _{C}{\vec {B}}\cdot d{\vec {l}}=\mu _{0}\int _{S}{\vec {J}}\cdot d{\vec {s}}+\mu _{0}\varepsilon _{0}{\frac {d}{dt}}\int _{S}{\vec {Y}}\cdot d{\vec {s}}$

Estos cuatro ecuaciones xunto cola fuercia de Lorentz son les qu'espliquen cualquier tipu de fenómenu electromagnéticu. Una fortaleza de les ecuaciones de Maxwell ye que permanecen invariantes en cualquier sistema d'unidaes, salvu de pequeñes esceiciones, y que son compatibles cola relatividá especial y xeneral. Amás Maxwell afayó que la cantidá $c={\frac {1}{\sqrt {\varepsilon _{0}\mu _{0}}}}$ yera a cencielles la velocidá de la lluz nel vacíu, polo que la lluz ye una forma de radiación electromagnético. Los valores aceptaos anguaño pa la velocidá de la lluz, la permitividad y la permeabilidá magnética resumir na siguiente tabla:

Símbolu	Nome	Valor numbéricu	Unidá de midida SI	Tipu
$c\$	$2,99792458\times 10^{8}$	definíu
$\ \varepsilon _{0}$	Permitividad del vacíu	$8,854\times 10^{-12}$	faradios por metro deriváu
$\ \mu _{0}\$	Permeabilidá magnética	$4\pi \times 10^{-7}$	henrios por metro definíu

Potencial esguilar y potencial vector

Artículu principal: Potencial vector magnéticu

De resultes matemática de les ecuaciones de Maxwell y amás coles mires de simplificar los sos cálculos introduciéronse los conceutos de potencial vector (${\vec {A}}$) y potencial esguilar ($\ \Phi$). Esti potencial vector nun ye únicu y nun tien significáu físicu claru pero sábese qu'un elementu infinitesimal de corriente da llugar a una contribución $d{\vec {A}}$ paralela a la corriente. Esti potencial llógrase de resultes de la llei de Gauss pal fluxu magnético, yá que se conoz que si la diverxencia d'un vector ye cero, esi vector de resultes define a un rotacional, asina:

$\nabla \cdot {\vec {B}}=\nabla \cdot (\nabla \times {\vec {A}})=0$

$\Longleftrightarrow \quad {\vec {B}}=\nabla \times {\vec {A}}$

A partir d'esti potencial vector y de la llei de Faraday puede definise un potencial esguilar asina:

${\begin{aligned}\nabla \times {\vec {Y}}&=-{\frac {\partial {\vec {B}}}{\partial {t}}}\\\nabla \times {\vec {Y}}+{\frac {\partial }{\partial {t}}}(\nabla \times {\vec {A}})&=0\\\nabla \times {\Big (}{\vec {Y}}+{\frac {\partial {\vec {A}}}{\partial {t}}}{\Big )}&=0\\\Longleftrightarrow \quad -\nabla \Phi &={\vec {Y}}+{\frac {\partial {\vec {A}}}{\partial {t}}}\end{aligned}}$

onde'l signu menos ($-$) ye por convención. Estos potenciales son importantes porque tienen una simetría gauge que nos da cierta llibertá a la d'escoyelos. El campu llétricu en función de los potenciales:

${\vec {Y}}=-\nabla \Phi -{\frac {\partial {\vec {A}}}{\partial {t}}}$

Topamos que cola introducción d'estes cantidaes les ecuaciones de Maxwell queden amenorgaes solo a dos, yá que, la llei de Gauss pal campu magnéticu y la llei de Faraday queden satisfeches por definición. Asina la llei de Gauss pal campu llétricu escrita en términos de los potenciales:

$-\nabla ^{2}\Phi -{\cfrac {\partial }{\partial t}}(\nabla \cdot {\vec {A}})={\cfrac {\rho }{\varepsilon _{0}}}$

y la llei de ampère xeneralizada

$\nabla (\nabla \cdot {\vec {A}})-\nabla ^{2}{\vec {A}}=\mu _{0}{\vec {J}}-\mu _{0}\varepsilon _{0}{\frac {\partial }{\partial t}}{\bigg (}\nabla \Phi +{\frac {\partial {\vec {A}}}{\partial t}}{\bigg )}$

Nótese que se pasó d'un conxuntu de cuatro ecuaciones diferenciales parciales de primer orde a solu dos ecuaciones diferenciales parciales pero de segundu orde. Sicasí, estes ecuaciones pueden simplificase con ayuda d'una fayadiza eleición del gauge.

Consecuencies físiques de les ecuaciones

Principiu de caltenimientu de la carga

Artículu principal: Carga llétrica

Les ecuaciones de Maxwell lleven implícites el principiu de caltenimientu de la carga. El principiu afirma que la carga llétrica nun se crea nin se destrúi, nin global nin llocalmente, sinón que namái se tresfier; y que si nuna superficie zarrada ta menguando la carga contenida nel so interior, tien d'haber un fluxu de corriente netu escontra l'esterior del sistema. Ye dicir la densidá de carga $\mathbf {\rho }$ y la densidá de corriente ${\vec {\jmath }}$ satisfaen una ecuación de continuidá.

A partir de la forma diferencial de la llei de Ampère tiense:

${\vec {\nabla }}\cdot \left({\vec {\nabla }}\times {\vec {B}}\right)=\mu _{0}{\vec {\nabla }}\cdot {\vec {J}}+\mu _{0}\varepsilon _{0}{\frac {\partial }{\partial t}}\left({\vec {\nabla }}\cdot {\vec {Y}}\right)$

que al reemplazar la llei de Gauss y tomar en cuenta que ${\vec {\nabla }}\cdot \left({\vec {\nabla }}\times {\vec {A}}\right)=0$ (pa cualquier vector ${\vec {A}}$), llógrase:

$0={\vec {\nabla }}\cdot {\vec {J}}+{\frac {\partial \rho }{\partial t}}$

o bien en forma integral: $0=\oint _{S}{\vec {J}}\cdot d{\vec {S}}+{\frac {dq}{dt}}$

Ecuaciones orixinales de Maxwell

Nel capítulu III de A Dynamical Theory of the Electromagnetic Field, tituláu "Ecuaciones xenerales del campu electromagnéticu", Maxwell formuló ocho ecuaciones que nomó de l'A a la H. Estes ecuaciones aportaron a conocíes como "les ecuaciones de Maxwell", pero agora esti epítetu recibir les ecuaciones qu'arrexuntó Heaviside. La versión de Heaviside de les ecuaciones de Maxwell realmente contién solo una ecuación de los ocho orixinales, la llei de Gauss que nel conxuntu d'ocho sería la ecuación G. Amás Heaviside fundió la ecuación A de Maxwell de la corriente total cola llei circuital de Ampère que nel trabayu de Maxwell yera la ecuación C. Esta fusión, que Maxwell por sigo mesmu publicó nel so trabayu On Physical Lines of Force de 1861 modifica la llei circuital de Ampère pa incluyir la corriente de desplazamientu de Maxwell.

Los ocho ecuaciones orixinales de Maxwell pueden ser escrites en forma vectorial asina:

Denominación	Nome	Ecuación
Llei de corrientes totales	${\vec {J}}_{\rm {tot}}={\vec {J}}+{\frac {\partial {\vec {D}}}{\partial t}}$
B	Definición de vector potencial magnéticu	$\mu {\vec {H}}={\vec {\nabla }}\times {\vec {A}}$
C	Llei circuital de Ampère	${\vec {\nabla }}\times {\vec {H}}={\vec {J}}_{\rm {tot}}$
D	Fuercia de Lorentz	${\vec {Y}}=\mu {\vec {v}}\times {\vec {H}}-{\frac {\partial {\vec {A}}}{\partial t}}-\nabla \phi$
Ecuación d'eletricidá elástica | ${\vec {Y}}={\frac {1}{\varepsilon }}{\vec {D}}$
F	Llei d'Ohm	${\vec {Y}}={\frac {1}{\sigma }}{\vec {J}}$
G	Llei de Gauss	${\vec {\nabla }}\cdot {\vec {D}}=\rho$
H	Ecuación de continuidá de carga	${\vec {\nabla }}\cdot {\vec {J}}=-{\frac {\partial \rho }{\partial t}}$

onde: ${\vec {H}}$ ye'l vector intensidá de campu magnéticu (llamáu por Maxwell como intensidá magnética); ${\vec {J}}$ ye la densidá de corriente llétrica y ${\vec {J}}_{\rm {tot}}$ ye la corriente total incluyida la corriente de desplazamientu; ${\vec {D}}$ ye'l campu desplazamientu (desplazamientu llétricu); $\ \rho$ ye la densidá de carga llibre (cantidá llibre d'eletricidá); ${\vec {A}}$ ye'l vector potencial magnéticu (impulsu magnéticu); ${\vec {Y}}$ ye'l campu llétricu (fuercia electromotriz [nun confundir cola actual definición de fuercia electromotriz]); $\ \phi$ ye'l potencial llétricu y $\ \sigma$ ye la conductividá llétrica (resistencia específica, agora solo resistencia).

Maxwell nun consideró a los medios materiales polo xeneral, esta formulación inicial usa la permitividad y la permeabilidá en medios lliniales, isótropos y non esvalixaos, a pesar que tamién se les puede usar en medios anisótropos.

Maxwell incluyó'l términu $\mu {\vec {v}}\times {\vec {H}}$ na espresión de la fuercia electromotriz de la ecuación D, que correspuende a la fuercia magnético por unidá de carga nun conductor que se mueve a una velocidá ${\vec {v}}$. Esto significa que la ecuación D ye otra formulación de la fuercia de Lorentz. Esta ecuación primero apaeció como la ecuación 77 de la publicación On Physical Lines of Force de Maxwell, anterior a la publicación de Lorentz. Na actualidá esta fuercia de Lorentz nun forma parte de les ecuaciones de Maxwell pero considerar una ecuación adicional fundamental nel electromagnetismu.

Espresión de les ecuaciones en relatividá

Na relatividá especial, les ecuaciones de Maxwell nel vacíu escribir por aciu unes rellaciones xeométriques, que tomen la mesma forma en cualesquier sistema de referencia inercial. Estes ecuaciones tán escrites en términos de cuadrivectores y tensores contravariantes, que son oxetos xeométricos definíos en M⁴. Estos oxetos rellacionar por aciu formes diferenciales en rellaciones xeométriques que al espresales en componentes de los sistemes coordenaos Lorentz apurren les ecuaciones pal campu electromagnéticu.

La cuadricorriente $\,J^{\alpha }$ ta descrita por una 1-forma y lleva la información sobre la distribución de cargues y corrientes. Los sos componentes son:

$\,J^{\alpha }=(c\rho (\mathbf {r} ,t),\mathbf {J} (\mathbf {r} ,t))$

Que tien de cumplir la siguiente rellación xeométrica por que se cumpla la ecuación de continuidá.

$\,\delta J=0$

Escritu en componentes de los sistemes coordenaos Lorentz queda:

$\partial _{\alpha }J^{\alpha }=0$

Pa poner en correspondencia objeto del mesmu rangu, utilízase'l operador de Laplace-Beltrami o laplaciana definida como:

$\Box =d\delta +\delta d$

Podemos poner en correspondencia'l cuadrivector densidá de corriente con otru oxetu del mesmu rangu como ye'l cuadripotencial, que lleva la información del potencial llétricu y el potencial vector magnéticu.

$\Box ^{2}A=-\mu _{0}J$

O escritu en coordenaes Lorentz llogramos que:

$\partial _{\mu }\partial ^{\mu }A^{\alpha }=\mu _{0}J^{\alpha }$

Espresión que reproduz les ecuaciones d'onda pa los potenciales electromagnéticos.

La 1-forma A lleva la información sobre los potenciales de los observadores inerciales siendo los sos componentes:

$A^{\alpha }=\left({\frac {\Phi }{c}},\mathbf {A} \right)$

Pa llograr l'oxetu xeométricu que contién los campos, tenemos que xubir el rangu d'A por aciu l'operador diferencial esterior $\partial$ llogrando la 2-forma F campu electromagnéticu. En forma xeométrica podemos escribir:

$\,F=da$

Qu'espresáu pa un sistema inercial Lorentz tenemos que:

$F^{\mu \nu }=\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu }$

Colo que llogramos el tensor de campu electromagnéticu.

$F^{\mu \nu }={\begin{bmatrix}0&-{\cfrac {Y_{x}}{c}}&-{\cfrac {Y_{y}}{c}}&-{\cfrac {Y_{z}}{c}}\\{\cfrac {Y_{x}}{c}}&0&-B_{z}&B_{y}\\{\cfrac {Y_{y}}{c}}&B_{z}&0&-B_{x}\\{\cfrac {Y_{z}}{c}}&-B_{y}&B_{x}&0\end{bmatrix}}$

Primer par d'ecuaciones de Maxwell

Les siguientes espresiones amiesten los campos coles fontes, rellacionamos la cuadricorriente col tensor campu electromagnéticu por aciu la forma xeométrica:

$\,\delta F=\mu _{0}J$

O bien en coordenaes Lorentz:

$\partial _{\mu }F^{\mu \nu }=\mu _{0}J^{\nu }$

Llogru de les ecuaciones

Pa un observable en S partiendo d'espresión en coordenaes Lorentz podemos llograr:

• Pa $\,\nu =0$ tenemos que: $\partial _{\mu }F^{\mu 0}=\mu _{0}J^{0}$, entós:

$\mu _{0}c\rho (\mathbf {r} ,t)=\partial _{1}F^{10}+\partial _{2}F^{20}+\partial _{3}F^{30}={\frac {1}{c}}\left[{\frac {\partial Y_{x}}{\partial x}}+{\frac {\partial Y_{y}}{\partial y}}+{\frac {\partial Y_{z}}{\partial z}}\right]$

Por tanto:

$\nabla \cdot \mathbf {Y} ={\frac {\rho (\mathbf {r} ,t)}{\varepsilon _{0}}}$

• Pa $\,\nu =1,2,3$ podemos llograr de la mesma forma que:

$\nabla \wedge \mathbf {H} =\mathbf {J} +{\frac {\partial \mathbf {D} }{\partial t}}$

Segundu par d'ecuaciones de Maxwell

Correspuenden a les ecuaciones homoxénees. Escrites en forma xeométrica tenemos que:

$\,\delta *F=0$

Que correspuende cola espresión nos sistemes coordenaos Lorentz:

$\,\partial _{\mu }*F^{\mu \nu }=0$

Onde'l tensor $\,*F$ ye'l tensor dual de F. Llograr por aciu l'operador de Hodge.

Llogru de les ecuaciones

• Pa $\,\nu =0$:

$\partial _{\mu }*F^{\mu 0}=\partial _{1}*F^{10}+\partial _{2}*F^{20}+\partial _{3}*F^{30}=\left[{\frac {\partial B_{x}}{\partial x}}+{\frac {\partial B_{y}}{\partial y}}+{\frac {\partial B_{z}}{\partial z}}\right]=0$

Por tanto:

$\nabla \cdot \mathbf {B} =0$

• Pa $\,\nu =1,2,3$ llógrase la ecuación vectorial:

$\nabla \wedge \mathbf {Y} +{\frac {\partial \mathbf {B} }{\partial t}}=0$

La propiedá $\,\partial _{\alpha }*F^{\alpha \beta }=0$ reproduz les ecuaciones de Maxwell internes, que puede espresase como $\,d\mathbf {F} =0$, que puede escribise nos sistemes coordenaos Lorentz como:

$\partial _{\gamma }F_{\alpha \beta }+\partial _{\beta }F_{\gamma \alpha }+\partial _{\alpha }F_{\beta \gamma }=0$

Podemos resumir el conxuntu d'espresiones que rellacionen los oxetos que describen el campu electromagnéticu na siguiente tabla. La primer columna son les rellaciones xeométriques, independientes de cualquier observador; la segunda columna son les ecuaciones descrites por aciu un sistema coordenáu Lorentz; y la tercera ye la descripción de la rellación y la llei que cumple.

Forma xeométrica	Covariante Lorentz	Descripción
$\,\delta A=0$	$\,\partial _{\mu }A^{\mu }=0$	Condición/gauge de Lorenz (*)
$\,F=dA$	$F^{\mu \nu }=\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu }$	Definición de Campos Electromagnéticos
$\Box A=\mu _{0}J$	$\partial _{\mu }\partial ^{\mu }A^{\alpha }=\mu _{0}J^{\alpha }$	Ecuaciones d'Ondes
${\begin{matrix}\delta F=\mu _{0}J\\\delta *F=0\end{matrix}}$	${\begin{matrix}\partial _{\mu }F^{\mu \nu }=\mu _{0}J^{\nu }\\\partial _{\mu }*F^{\mu \nu }=0\end{matrix}}$	Ecuaciones de Maxwell
$\,\delta J=0$	$\partial _{\alpha }J^{\alpha }=0$	Llei de caltenimientu de la Carga

(*) Esiste un tracamundiu habitual tocantes a la nomenclatura d'esti gauge. Les primeres ecuaciones nes qu'apaez tal condición (1867) deber a Ludvig V. Lorenz, non al muncho más conocíu Hendrik A. Lorentz. (Vease: J.D. Jackson: Classical Electrodynamics, 3rd edition p.294)

Finalmente'l cuadrigradiente defínese asina:

${\partial \over {\partial x^{\alpha }}}\ {\stackrel {\mathrm {def} }{=}}\ \partial _{\alpha }\ {\stackrel {\mathrm {def} }{=}}\ {}_{,\alpha }\ {\stackrel {\mathrm {def} }{=}}\ \left({\frac {\partial }{\partial ct}},\nabla \right)$

Los índices repitíos sumir d'alcuerdu al conveniu de sumación d'Einstein. Acordies con el cálculu tensorial, los índices pueden xubise o baxase per mediu de la matriz fundamental g.

El primer tensor ye una espresión de dos ecuaciones de Maxwell, la llei de Gauss y la llei de Ampère xeneralizada; la segunda ecuación ye consecuentemente una espresión de les otres dos lleis.

Suxirióse que'l componente de la fuercia de Lorentz $\ {\vec {v}}\times {\vec {B}}$ puede derivase de la llei de Coulomb y por eso la relatividá especial asume la invarianza de la carga llétrica.

Espresión de les ecuaciones pa una frecuencia constante

Nes ecuaciones de Maxwell, los campos vectoriales nun son solo funciones de la posición, polo xeneral son funciones de la posición y del tiempu, como por casu ${\vec {H}}(x,y,z,t)$. Pal resolución d'estes ecuaciones en derivaes parciales, les variables posicionales atopar cola variable temporal. Na práutica, la resolución de diches ecuaciones pueden contener una solución harmónica (sinusoidal).

Con ayuda de la notación complexa puede evitase la dependencia temporal de los resultaos harmóniques, esaniciando asina'l factor complexu de la espresión $\ y^{i\omega t}$. Gran parte de les resoluciones de les ecuaciones de Maxwell tomen amplitúes complexes, amás de nun ser solo función de la posición. En llugar de la derivación parcial nel tiempu tiense la multiplicación del factor imaxinariu $\ i\omega$, onde $\ \omega$ ye la frecuencia angular.

Na forma complexa, les ecuaciones de Maxwell tomen la siguiente forma:

${\vec {\nabla }}\cdot {\vec {D}}=\rho$

${\vec {\nabla }}\cdot {\vec {B}}=0$

${\vec {\nabla }}\times {\vec {Y}}=-i\omega {\vec {B}}$

${\vec {\nabla }}\times {\vec {H}}={\vec {\imath }}=(\sigma +i\omega \varepsilon ){\vec {Y}}$

Ver tamién

• Electromagnetismu
• James Clerk Maxwell, Oliver Heaviside
• Carga
• Onda electromagnética, ecuación d'onda electromagnética
• Ecuaciones de Jefimenko
• Llei de Gauss, Llei de Faraday, Llei de Ampère
• Diverxencia, Rotacional
• Teoría del absorbedor de Wheeler-Feynman

Enllaces esternos

• On Physical Lines of Force
• Wikisource n'inglés contién obres orixinales de o sobre Ecuaciones de Maxwell.
• Monografíes.com archivu sobre ecuaciones de Maxwell
• Modelu de Maxwell
• Fundamentos de la radiación
• A treatise on electricity and magnetism (1873) Vol. 1 PDF
• A treatise on electricity and magnetism (1873) Vol. 2 PDF

• Datos: Q51501
• Multimedia: Maxwell's equations