Potenciación

La potenciación ye una operación matemática ente dos términos denominaos: base a y esponente n. Escríbese aⁿ y lléese usualmente como «a eleváu a n» o tamién «a eleváu a la n». Hai dellos númberos esponentes especiales como'l 2, que se llee al cuadráu o'l 3, que-y correspuende al cubu. Tien de notase que nel casu de la potenciación la base y l'esponente pueden pertenecer a conxuntos distintos, nun aniellu totalmente xeneral la base va ser un elementu del aniellu pero l'esponente va ser un númberu natural que nun tien por qué pertenecer al aniellu. Nun cuerpu l'esponente puede ser un númberu enteru.

Potenciación
hiperoperación (es)
operación binaria

Gráfica d'una función Gráfica de delles funciones potencia.

Definición

Llámase potencia a una espresión de la forma $a^{n}$, onde a ye la base y n ye'l esponente. La so definición varia según el conxuntu numbéricu al que perteneza l'esponente.

Esponente enteru

Cuando l'esponente ye un númberu natural n, este indica les vegaes qu'apaez a multiplicando por sigo mesmu, siendo a un númberu cualesquier:

(1)${\begin{array}{ll}a^{1}=&a\\a^{2}=&a\times a\\\vdots &\vdots \\a^{n}=&\underbrace {a\times \cdots \times a} _{n{\text{ vegaes}}},\end{array}}$

Esta definición puede aplicase, tantu a númberos reales o complexos, según a otres estructures alxebraiques más astractes, como pueden ser, por casu, matrices cuadraes.

Multiplicación de potencies d'igual base

El productu de dos potencies que tienen la mesma base ye igual a una potencia de dicha base que tien como esponente la suma de los esponentes, esto ye:

$a^{n}\cdot a^{m}=a^{n+m}$

$a^{n}\times a^{m}=\underbrace {\underbrace {a\times \cdots \times a} _{n}\times \underbrace {a\times \cdots \times a} _{m}} _{n+m}=a^{n+m}$

Exemplos:

$9^{3}\cdot 9^{2}=9^{3+2}=9^{5}$

Potencia d'una potencia

La potencia d'una potencia de base a ye igual a la potencia de base a y que'l so esponente ye'l productu de dambos esponentes (la mesma base y multiplíquense los esponentes):

${(a^{m})}^{n}=a^{m\cdot n}$

$(a^{m})^{n}={(\underbrace {a\times \cdots \times a} _{m})}^{n}=n{\begin{cases}\underbrace {\begin{matrix}a\times &\cdots &\times a\times \\\vdots &&\vdots \\a\times &\cdots &\times a\end{matrix}} _{m}\end{cases}}=a^{m\cdot n}$

Por cuenta de esto, la notación $a^{b^{c}}$ acutar pa significar $a^{(b^{c})}$ yá que ${(a^{b})}^{c}$ puede escribise cenciellamente como $a^{bc}\,$.

Potencia d'un productu

La potencia d'un productu ye igual al productu de cada unu de los factores eleváu al mesmu esponente, esto ye:

$(a\cdot b)^{n}=a^{n}\cdot b^{n}$

$(a\times b)^{n}=n{\begin{cases}{\begin{matrix}a\times b\times \\\vdots \\a\times b\end{matrix}}\end{cases}}=a^{n}\times b^{n}$

---

Si la base a tien inversu aditivu, indicáu por aciu signu negativu -a, entós tiense la regla:

$(-a)^{n}=\;\;\;\;\;a^{n}$ si n ye par. $(-a)^{n}=-(a^{n})$ si n ye impar.

${\begin{array}{ll}(-a)^{1}=&-a\\(-a)^{2}=&(-a)\times (-a)=a^{2}\\(-a)^{3}=&\underbrace {(-a)\times (-a)} _{a^{2}}\times (-a)=-(a^{3})\\\vdots &\\(-a)^{n}=&\underbrace {((-a)\times (-a))\times \cdots \times ((-a)\times (-a))} _{n{\text{ par}}}=a^{n}\\(-a)^{n}=&\underbrace {\underbrace {((-a)\times (-a))\times \cdots \times ((-a)\times (-a))} _{n-1{\text{ par por tanto ye }}a^{n-1}}\times (-a)} _{n{\text{ impar}}})=-(a^{n}),\end{array}}$

Si la base a tien inversu multiplicativu c, ye dicir c·a = 1 o que $c={\frac {1}{a}}$, entós esti se denota por $a^{-1},$ y l'esponente puede ampliase a tolos númberos enteros:

(2)${\begin{array}{l}a^{-1}={\frac {1}{a}}\\a^{-n}={\frac {1}{a^{n}}}\end{array}}$

Observación

$a^{-n}=(a^{-1})^{n}=\underbrace {{\frac {1}{a}}\times \cdots \times {\frac {1}{a}}} _{n}={\frac {1}{\underbrace {a\times \cdots \times a} _{n}}}={\frac {1}{a^{n}}}.$

División de potencies d'igual base

El cociente de dos potencies cola mesma base ye igual a una potencia de dicha base con un esponente igual a la diferencia del esponente del dividendu menos el del divisor, esto ye:

${\frac {a^{m}}{a^{n}}}=a^{m-n}$

${\frac {a^{m}}{a^{n}}}=a^{m}\cdot a^{-n}$ $=a^{m+(-n)}$ $=a^{m-n}$ De forma estendida apaecen tres caso: $={\frac {\overbrace {a\times \cdots \times a} ^{m}}{\underbrace {a\times \cdots \times a} _{n}}}$ Fallu al revisar la fórmula (función '\canciellu' desconocida): {\displaystyle =\begin{cases}\begin{matrix} \frac{ \overbrace{\canciellu a \times \cdots \times \canciellu a}^n \times \overbrace{a \times \cdots \times a}^{m-n}}{\underbrace{\canciellu a \times \cdots \times \canciellu a}_n}=a^{m-n} & \text{Si } m>n\\ \frac{ \overbrace{ \canciellu a \times \cdots \times \canciellu a}^m }{\underbrace{ \canciellu a \times \cdots \times \canciellu a}_n}=1& \text{Si } m=n\\ \frac{ \overbrace{ \canciellu a \times \cdots \times \canciellu a}^m }{\underbrace{ \canciellu a \times \cdots \times \canciellu a}_m \times \underbrace{a \times \cdots \times a}_{n-m} }=\frac{1}{a^{n-m}}& \text{Si } m<n \end{matrix}\end{cases}}

Exemplu:

${\frac {9^{5}}{9^{3}}}=9^{5-3}=9^{2}$

Potencia d'esponente 0

Un númberu distintu de 0 eleváu al esponente 0 da como resultáu la unidá (1), yá que:

$1={\frac {a^{n}}{a^{n}}}=a^{n-n}=a^{0}\,$

El casu particular de $0^{0}\,$ nun ta definíu y ye conocíu como una indetermín.

Potencia d'un cociente

La potencia d'un cociente ye igual al cociente de cada unu de los númberos eleváu al mesmu esponente.

$\left({\frac {a}{b}}\right)^{n}={\frac {a^{n}}{b^{n}}}$

$\left({\frac {a}{b}}\right)^{n}=$$\left(a\cdot b^{-1}\right)^{n}=$ $a^{n}\cdot b^{-n}=$ ${\frac {a^{n}}{b^{n}}}$ O de forma estendida: $=\underbrace {{\frac {a}{b}}\times \cdots \times {\frac {a}{b}}} _{n}={\frac {a\times \cdots \times a}{b\times \cdots \times b}}={\frac {a^{n}}{b^{n}}}$

---

Si la base a = 0, entós a nun tien inversu multiplicativu $a^{-1}$, polo que namái se presenten esponentes de númberos naturales por (1) quedando asina prohibida la notación (2) como valor numbéricu:

$0^{1}=0$

$0^{n}=\underbrace {0\times \cdots \times 0} _{n}=0.$

Esponente racional

Artículu principal: Radicación

La potenciación con esponente racional vien de la necesidá de resolver una ecuación del tipu $x^{n}=a$, de manera que $x={\sqrt[{n}]{a}}$, pero haber de garantizar que dicha x sía un númberu real y esto namái puede garantizase pa tou n si la base a ye un númberu real positivu, polo qu'esiste un teorema que diz:

Dau un númberu real positivu a, este tien una única raíz n-ésima positiva.

Pa notar la raíz defínese l'usu de fracciones nel esponente:

(3)$a^{\frac {1}{n}}={\sqrt[{n}]{a}}$

Observación

$\left(a^{\frac {1}{n}}\right)^{n}=a^{{\frac {1}{n}}\cdot n}=a^{1}=a.$

Polo xeneral pa les fracciones defínese que:

(4)${\begin{array}{ll}a^{\frac {n}{m}}&={\sqrt[{m}]{a^{n}}}\\a^{-{\frac {n}{m}}}&={\frac {1}{a^{\frac {n}{m}}}}\end{array}}$

Rellación

$a^{\frac {n_{1}}{m_{1}}}=a^{\frac {n_{2}}{m_{2}}}\Leftrightarrow$ ${\frac {n_{1}}{m_{1}}}={\frac {n_{2}}{m_{2}}}$

${\frac {n_{1}}{m_{1}}}={\frac {n_{2}}{m_{2}}}\Rightarrow$ $n_{1}\cdot m_{2}=n_{2}\cdot m_{1}$ $a^{\frac {n_{1}}{m_{1}}}=a^{\frac {n_{2}}{m_{2}}}\Leftrightarrow$ $\left(a^{\frac {n_{1}}{m_{1}}}\right)^{m_{1}\cdot m_{2}}=\left(a^{\frac {n_{2}}{m_{2}}}\right)^{m_{1}\cdot m_{2}}\Leftrightarrow$ $a^{n_{1}\cdot m_{2}}=a^{m_{1}\cdot n_{2}}.$

Propiedaes

$a^{\frac {n_{1}}{m_{1}}}\cdot a^{\frac {n_{2}}{m_{2}}}=a^{{\frac {n_{1}}{m_{1}}}+{\frac {n_{2}}{m_{2}}}},$

$\left(a^{\frac {n_{1}}{m_{1}}}\right)^{\frac {n_{2}}{m_{2}}}=a^{{\frac {n_{1}}{m_{1}}}\cdot {\frac {n_{2}}{m_{2}}}},$

$(a\cdot b)^{\frac {n}{m}}=a^{\frac {n}{m}}\cdot b^{\frac {n}{m}}.$

Esponente real

Artículos principales: Exponenciación y Llogaritmu

La potenciación puede estendese a esponentes reales usando socesiones racionales; esto recuéyese nel siguiente teorema:

Dau un númberu real positivu a y una socesión de númberos racionales $q_{n}$ que tien llende b, entós esiste'l llende d'una socesión llende de la socesión $a^{q_{n}}$ que s'escribe como: $a^{b}=\lim _{n\to \infty }a^{q_{n}}$

Nótese que los socesivos aproximamientos de a^b tienen como esponente númberos racionales, colo que por que la definición sía consistente, esíxese que a sía un númberu real positivu.

Análogamente, puede estendese la potenciación a funciones, usando la función esponencial, y la so inversa, la función llogaritmu natural, nun procesu que se denomina exponenciación. Asina, defínese

$f(x)^{g(x)}=y^{g(x)\ln f(x)}$.

Otramiente, esta ye totalmente consistente si'l conxuntu imaxe de f(x) ye'l conxuntu de los númberos reales positivos R₊, o dalgún subconxuntu d'este, siendo los valores de la función esponente g(x) númberos reales cualesquier, por cuenta de que'l llogaritmu natural nun ta definíu pa númberos negativos.

Propiedaes

$a^{b}\cdot a^{c}=a^{b+c},$

$\left(a^{b}\right)^{c}=a^{b\cdot c},$

$(a\cdot b)^{c}=a^{c}\cdot b^{c}.$

Esponente complexu

Puede estendese a esponentes complexos usando funciones analítiques o holomorfas, asina $a^{b}={\mbox{det-exp}}(b\cdot {\mbox{det-log }}a)$ onde det-exp ye la determinación de la esponencial y det-log la determinación del llogaritmu.

Resultaos de potenciación

Propiedaes que non cumple la potenciación

Nun ye distributiva con al respective de la adición y sustracción (vease productos notables), esto ye, nun puede distribuyise cuando dientro del paréntesis ye suma o resta:

$(a+b)^{m}\ \neq \ a^{m}+b^{m}$

$(a-b)^{m}\ \neq \ a^{m}-b^{m}$

Nun cumple la propiedá conmutativa:

$a^{b}\ \neq \ b^{a}$

Tampoco cumple la propiedá asociativa:

$a^{b^{c}}=a^{(b^{c})}\neq (a^{b})^{c}=a^{(b\cdot c)}=a^{bc}$

Potencia de base 10

Artículu principal: Notación científica

Pa les potencies con base 10 y esponente enteru, l'efectu va ser mover la coma decimal tantes posiciones como indique l'esponente, escontra la esquierda si l'esponente ye negativu, o escontra la derecha si l'esponente ye positivu.

Exemplos:

${\begin{array}{lcl}10^{-6}&=&0,000001\\10^{-5}&=&0,00001\\10^{-4}&=&0,0001\\10^{-3}&=&0,001\\10^{-2}&=&0,01\\10^{-1}&=&0,1\end{array}}$

${\begin{array}{lcr}10^{0}&=&1\\10^{1}&=&10\\10^{2}&=&100\\10^{3}&=&1.000\\10^{4}&=&10.000\\10^{5}&=&100.000\\10^{6}&=&1.000.000\end{array}}$

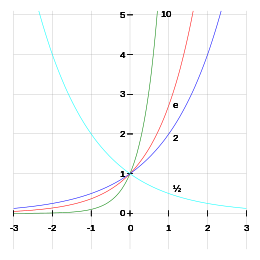
Representación gráfica

La representación gráfica d'una función potencia f(x) = xⁿ con esponente natural n par tien una simetría similar a la d'una parábola. El so vértiz asitiar nel puntu (0, 0) y la curva ye decreciente nel segundu cuadrante y creciente nel primeru.

La representación gráfica d'una función potencia f(x) = xⁿ con esponente natural n impar ye una curva con dos rames xuníes nel puntu (0, 0), que tien simetría rotacional alredor d'este. El puntu d'inflexón precisamente atópase nel puntu (0, 0), la curva ye siempres creciente y ocupa el tercer y primer cuadrante.

Estes curves son continues y derivables en tol so dominiu de definición.

Gráficu d'una parábola$y=x^{2}\,$. Gráficu d'una parábola$y=x^{2}\,$.   Gráficu de $y=x^{3}\,$. Gráficu de $y=x^{3}\,$.

Llendes

Indetermín 0⁰

El casu especial $0^{0}\,$considérase indefiníu y dependiendo del contestu pueden ser asignaos distintos valores dependiendo de les propiedaes específiques que quieran caltenese.

Por casu, puede argumentase que $0^{0}\,$ye l'igual al valor de la llende :$\lim _{x\to 0^{+}}x^{0}$ y como $x^{0}=1$ pa $x\neq 0$, dichu valor podría ser igual a 1. Sicasí tamién puede considerase dicha espresión como'l valor de la llende :$\lim _{x\to 0^{+}}0^{x}$ y como $0^{x}=0$ pa $x\neq 0$, dichu valor podría ser igual a 0. Esto ilustra que la forma $0^{0}\,$ puede corresponder a distintos valores y por ello considérase indefinida.

L'alderique sobre'l valor de la forma $0^{0}\,$ tien casi dos sieglos d'antigüedá. Mientres los primeros díes del analís matemáticu en que'l fundamentu formal del cálculu nun s'estableciera, yera común aceptar que $0^{0}\,$=1. Sicasí, en 1821 cuando Cauchy publica'l Cours d'Analyse de l'École Royale Polytechnique estableciendo'l primer tratamientu rigorosu del analís, dicha forma apaez nuna tabla de formes indefiníes xunto a otres como 0/0. Nos años 1830, Libri publicó un argumentu p'asignar 1 como valor de $0^{0}\,$ y Möbius sofitar afirmando equivocadamente que :$\lim _{t\to 0^{+}}f(t)^{g(t)}=1\,$ siempres que $\lim _{t\to 0^{+}}f(t)=\lim _{t\to 0^{+}}g(t)=0.$ Sicasí una comentarista que robló a cencielles como «S» apurrió un contraejemplo

$f(t)^{g(t)}={(y^{-1/t})}^{t}$

que la so llende cuando $t\to 0^{+}$ ye $1/y$, lo cual aseló l'alderique cola aparente conclusión del incidente que $0^{0}\,$ tendría de permanecer indefinida. Pueden atopase más detalles en Knuth (1992).

Na actualidá, suel considerase la forma $0^{0}\,$ como indefinida y nun se-y asigna valor si nun se tien un contestu nel cual el valor asignáu tenga sentíu.

Pa calcular llendes que'l so valor aparente ye $0^{0}\,$ suel usase la regla de l'Hôpital.

Xeneralizaciones

Estensión a estructures astractes

La definición de potenciación puede estendese a esponentes reales, complexos o inclusive matriciales. Dau un aniellu $\scriptstyle (\mathbb {A} ,+,\cdot )$ la operación de potenciación defínese como:

${\begin{array}{rccl}\mathrm {Pot} :&\mathbb {A} \times \mathbb {N} &\longrightarrow &\mathbb {A} \\&(x,n)&\longrightarrow &y=\mathrm {Pot} (x,n)=x^{n}\end{array}}$

Esto difier de la exponenciación que ye definible sobre un cuerpu que contenga a los racionales o ciertes álxebres sobre los reales o complexos:

${\begin{array}{rccl}\mathrm {Exp} :&\mathbb {A} &\longrightarrow &\mathbb {A} \\&x&\longrightarrow &y=\mathrm {Exp} (x)=y^{x}\end{array}}$

$\mathrm {Exp} (x)=\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}}$

Obviamente la exponenciación namái puede definise sobre un conxuntu nel que sía posible definir la potenciación, anque un aniellu va almitir siempres la operación de potenciación (con esponente natural) anque nun almita la exponenciación.

Potencia de númberos complexos

Artículu principal: Fórmula de De Moivre

Pa cualesquier de los númberos reales $a,b,c,d\,$ tiense la identidá:

$\left(a\,y^{i\,b}\right)^{\left(c\,y^{i\,d}\right)}=a^{c\,\cos d}\,y^{i\,\left(c\,\log a\,\sin d+b\,c\,\cos d\right)-b\,c\,\sin d}$

Ver tamién

• Productos notables
• raíz cuadrada
• Radicación
• Fórmula de De Moivre (pa potencies de númberos complexos)
• Potencia de dos
• Serie de potencies

Bibliografía

• Ortega, Joaquín M. (1993). «Potencies de base real positiva y esponente real», analís matemáticu.html?id=dmOd2KMy7eYC Introducción al analís matemáticu. Barcelona: Universidá Autónoma de Barcelona/Labor, páx. 51-54. ISBN 978-8-433-53047-9.

Enllaces esternos

• Artículu sobre potenciación n'Enciclopedia universal n'español Archiváu 2018-06-16 en Wayback Machine

• Datos: Q33456
• Multimedia: Exponentiation

• Datos: Q33456
• Multimedia: Exponentiation