Integración

La integración ye un conceutu fundamental del cálculu y del analís matemáticu. Básicamente, una integral ye una xeneralización de la suma d'infinitos sumandos, infinitamente pequeños.

Integración
conceutu matemáticu
aplicación lineal (es) y operación unaria (es)

La integral definida d'una función representa l'área llindada pola gráfica de la función, nun sistema de coordenaes cartesianes con signu positivu cuando la función toma valores positivos y signu negativu cuando toma valores negativos.

El cálculu integral, encuadráu nel cálculu infinitesimal, ye una caña de les matemátiques nel procesu d'integración o antiderivación. Ye bien común na inxeniería y na ciencia; utilízase principalmente pal cálculu d'árees y volúmenes de rexones y sólidos de revolución.

Foi usáu per primer vegada por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz y Isaac Barrow. Los trabayos d'esti postreru y apurrir de Newton xeneraron el teorema fundamental del cálculu integral, que propón que la derivación y l'integración son procesos inversos.

Principales oxetivos del cálculu integral

Los sos principales oxetivos a estudiar son:

• Área d'una rexón plana
• Cambéu de variable
• Integrales indefiníes
• Integrales definíes
• Integrales impropies
• Integral de llinia
• Integrales múltiples (dobles o triples)
• Integrales trigonométriques, logarítmiques y esponenciales
• Métodos d'integración
• Teorema fundamental del cálculu
• Volume d'un sólidu de revolución

Teoría

$\scriptstyle \ \int _{a}^{b}f(x)\,\mathrm {d} x$ interprétase como l'área so la curva de f, ente a y b.

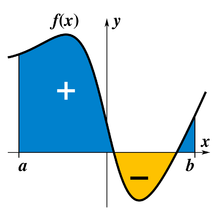
Dada una función $f(x)$ d'una variable real $x$ y un intervalu $[a,b]$ de la recta real, la integral ye igual al área de la rexón del planu $xy$ llindada ente la Gráfica d'una función gráfica de $f$, la exa $x$, y les llinies verticales $x=a$ y $x=b$, onde son negatives les árees per debaxo de la exa $x$.

$\int _{a}^{b}f(x)\,{\text{d}}x$

La pallabra "integral" tamién puede faer referencia a la noción de primitiva: una función F, que la so derivada ye la función dada $f$. Nesti casu denominar integral indefinida, ente que les integrales trataes nesti artículu son les integrales definíes. Dellos autores caltienen una distinción ente integrales primitives ya indefiníes.

Qué ye la integral (animación)

Los principios de la integración fueron formulaos por Newton y Leibniz a finales del sieglu XVII. Al traviés del teorema fundamental del cálculu, que desenvolvieron los dos de forma independiente, la integración coneutar cola derivación, y l'integral definida d'una función puede calculase fácilmente una vegada conozse una antiderivada. Les integrales y les derivaes pasaron a ser ferramientes básiques del cálculu, con numberoses aplicaciones en ciencia ya inxeniería.

Bernhard Riemann dio una definición rigorosa de la integral. Basar nun Llende d'una función llende qu'avera l'área d'una rexón curvillinia a base de partila en pequeños cachos verticales. A empiezos del sieglu XIX, empezaron a apaecer nociones más sofisticaes de la integral, onde se xeneralizaron los tipos de les funciones y los dominios sobre los cualos faise la integración. La integral curvillinia definir pa funciones vectoriales d'una variable, y l'intervalu d'integración [a,b] sustituyir pol de la parametrización de la curva sobre la cual tase integrando, que, coneuta dos puntos del planu o del espaciu. Nuna integral de superficie, la curva sustituyir por un cachu d'una superficie nel espaciu tridimensional.

Les integrales de les formes diferenciales desempeñen un papel fundamental na xeometría diferencial moderna. Estes xeneralizaciones de la integral surdieron primero a partir de les necesidaes de la física, y tienen un papel importante na formulación de munches lleis físiques cómo, por casu, les del electromagnetismu. Los conceutos modernos d'integración basar na teoría matemática astracta conocida como integral de Lebesgue, que foi desenvuelta por Henri Lebesgue.

Historia

Integración antes del cálculu

La integración puede trazase nel pasáu hasta'l antiguu Exiptu, circa 1800 e. C., col papiru de Moscú, onde se demuestra que yá se conocía una fórmula pa calcular el volume d'un tueru piramidal. La primer téunica sistemática documentada capaz de determinar integrales ye'l métodu de exhausción d'Eudoxo (circa 370 e. C.), que trataba d'atopar árees y volúmenes a base de partilos nun númberu infinitu de formes pa les cualos conociérense l'área o'l volume. Esti métodu foi desenvueltu y usáu más palantre por Arquímedes, que lo emplegó pa calcular árees de paráboles y un aproximamientu al área del círculu. Métodos similares fueron desenvueltos de forma independiente en China alredor del sieglu III por Liu Hui, que los usó p'atopar l'área del círculu. Más tarde, Zu Chongzhi usó esti métodu p'atopar el volume d'una esfera. Nel Siddhanta Shiromani, un llibru d'astronomía del sieglu XII del matemáticu indiu Bhaskara II, atópense delles idees de cálculu integral.

Hasta'l sieglu XVI nun empezar a apaecer adelantos significativos sobre'l métodu de exhausción. Nesta dómina, per un sitiu, col trabayu de Cavalieri col so métodu de los indivisibles y, per otru llau, colos trabayos de Fermat, empezar a desenvolver los fundamentos del cálculu modernu. A empiezos del sieglu XVII, produciéronse nuevos adelantos coles aportaciones de Barrow y Torricelli, que presentaron los primeros nicios d'una conexón ente la integración y la derivación.

Newton y Leibniz

Los principales adelantos n'integración vinieron nel sieglu XVII cola formulación del teorema fundamental del cálculu, realizáu de manera independiente por Newton y Leibniz. El teorema demuestra una conexón ente la integración y la derivación. Esta conexón, combinada cola facilidá, comparativamente falando, del cálculu de derivaes, puede usase pa calcular integrales. En particular, el teorema fundamental del cálculu dexa resolver una clase más amplia de problemes. Tamién cabo destacar tol marcu estructural alredor de les matemátiques que desenvolvieron tamién Newton y Leibniz. El llamáu cálculu infinitesimal dexó analizar, de forma precisa, funciones con dominios continuos. Darréu, esti marcu evolucionó escontra'l cálculu modernu, que la so notación pa les integrales procede direutamente del trabayu de Leibniz.

Formalización de les integrales

Anque Newton y Leibniz apurrieron un enfoque sistemáticu a la integración, el so trabayu escarecía d'un ciertu nivel de rigor. Ye memorable la espresión del obispu Berkeley interpretando los infinitesimales como los "pantasmes de les cantidaes que s'esmorecen".

El cálculu adquirió una posición más firme col desenvolvimientu de los Llende d'una función llendes y, na primer metá del sieglu XIX, recibió una fundamentación fayadiza per parte de Cauchy. La integración foi rigorosamente formalizada per primer vegada por Riemann, emplegando llendes. A pesar de que toles funciones continues estazaes y acutaes son integrables nun intervalu acutáu, más tarde consideráronse funciones más xenerales pa les cualos la definición de Riemann nun yera aplicable y por tanto nun yeren integrables nel sentíu de Riemann. Darréu Lebesgue dio una definición distinta de la integral basada na teoría de la midida que xeneralizaba la definición de Riemann, asina toa función integrable nel sentíu de Riemann tamién lo ye nel sentíu de Lebesgue, anque esisten delles funciones integrables nel sentíu de Lebesgue que nun lo son nel sentíu de Riemann. Más apocayá propunxéronse otres definiciones d'integral entá más xenerales, qu'amplíen les definiciones de Riemann y Lebesgue.

Notación

El símbolu d'integral n'escritos (d'esquierda a derecha) ingleses, alemanes y rusos.

Isaac Newton usaba una pequeña barra vertical enriba d'una variable pa indicar integración, o ponía la variable dientro d'una caxa. La barra vertical confundíase fácilmente con ${\dot {x}}$ o $x'\,\!$, que Newton usaba pa indicar la derivación, y amás la notación "caxa" yera malo de reproducir polos imprentadores; por ello, estes notaciones nun fueron llargamente adoptaes.

La notación moderna de les integrales indefiníes foi presentada por Gottfried Leibniz en 1675. Pa indicar summa (ſumma; en llatín, "suma" o "total"), afixo'l símbolu integral, "∫", a partir d'una lletra S allargada porque consideraba a la integral como una suma infinita de addendas infinitesimales. La notación moderna de la integral definida, coles llendes enriba y embaxo del signu integral, usar por primer vegada Joseph Fourier en Mémoires de l'Academia Francesa, alredor de 1819-20, reimpresa nel so llibru de 1822.

Esisten llixeres diferencies na notación del símbolu de la integral na lliteratura de les diverses llingües: el símbolu inglés ta inclináu escontra la derecha, n'alemán tradicionalmente escribióse derechu (ensin enclín) mientres la variante rusa tradicional ta inclinada escontra la esquierda.

Na notación matemática n'árabe modernu, que s'escribe de derecha a esquierda, úsase un signu integral invertíu .

Xeneralizaciones modernes

Tres la creación del cálculu integral a partir del sieglu XVII, y el so desenvolvimientu más o menos intuitivu mientres un par de sieglos, la noción d'integración foi analizada con mayor rigor mientres el sieglu XIX. Asina la primer noción rigorosa d'integración ye'l conceutu d'integral de Riemann, según la so xeneralización conocida como integral de Riemann-Stieltjes. A principios del sieglu XX, el desenvolvimientu de la teoría de la midida llevó al conceutu más xeneral y cualitativamente más avanzáu d'integral de Lebesgue. Más tarde el desenvolvimientu de la noción de procesu estocástico dientro de la teoría de la probabilidá llevó a la formulación de la integral de Itō escontra'l final de la primer metá del sieglu XX, y darréu a la so xeneralización conocida como integral de Skorohod (1975). Coles mesmes dende los años 1960, buscóse definición matemáticamente rigorosa d'integral de caminos cuánticos.

Terminoloxía y notación

Si una función tien una integral, dizse que ye integrable. De la función de la cual calcúlase la integral dizse que ye'l integrando. Denominar dominiu d'integración a la rexón sobre la cual intégrase la función. Si la integral nun tien un dominiu d'integración, considérase indefinida (la que tien dominiu considérase definida). Polo xeneral, l'integrando pue ser una función de más d'una variable, y el dominiu d'integración puede ser una área, un volume, una rexón de dimensión cimera, o inclusive un espaciu astractu que nun tien estructura xeométrica en nengún sentíu avezáu.

El casu más senciellu, la integral d'una función real f d'una variable real x sobre l'intervalu [a, b], escríbese

$\int _{a}^{b}f(x)\,{\text{d}}x$

El signu ∫, una "S" allargada, representa la integración; a y b son el llende inferior y el llende cimera de la integración y definen el dominiu d'integración; f ye l'integrando, que se tien qu'evaluar al variar x sobre l'intervalu [a,b]; y dx puede tener distintes interpretaciones dependiendo de la teoría que s'emplegue. Por casu, puede trate a cencielles como una indicación de que x ye la variable d'integración, como una representación de los pasos na suma de Riemann, una midida (na integración de Lebesgue y les sos estensiones), un infinitesimal (n'analís non estándar) o como una cantidá matemática independiente: una forma diferencial. Los casos más complicaos pueden variar la notación llixeramente.

Conceutos y aplicaciones

Aproximamientos a la integral de ${\sqrt {x}}$ ente 0 y 1, con ■ 5 muestres pela izquierda (enriba) y ■ 12 muestres pela derecha (embaxo).

Les integrales apaecen en munches situaciones práutiques. Considérese una piscina. Si ye rectangular y de fondura uniforme, entós, a partir del so llargor, anchor y fondura, puede determinase fácilmente'l volume d'agua que puede contener (pa enllenala), l'área de la superficie (pa cubrir), y el llargor del so cantu (si ríquese saber la so midida). Pero si ye ovalada con un fondu arrondáu, les cantidaes anteriores nun son sencielles de calcular. Una posibilidá ye calculales por aciu integrales.

Pal cálculu integral d'árees sigue'l siguiente razonamientu:

1. Por casu, consideremos la curva amosada na figura de riba, gráfica de la función $y=f(x)={\sqrt {x}}\,$, acutada ente $x=0\,$ y $x=1\,$.
2. La respuesta a la entruga ¿Cuál ye l'área so la curva de función $f\,$, nel intervalu dende $0\,$ hasta $1\,$? ye: que l'área va coincidir cola integral de $f\,$. La notación pa esta integral va ser

$\int _{0}^{1}{\sqrt {x}}\,{\text{d}}x\,\!$.

Un primer aproximamientu, anque non bien precisa, pa llograr esta área, consiste en determinar l'área del cuadráu unidá que'l so llau dar la distancia dende x=0 hasta x=1 o tamién el llargor ente y=f(0)=0 y y=f(1)=1. El so área ye esautamente 1x1 = 1. Tal como puede inferise, el verdaderu valor de la integral va tener que ser más pequeñu. Particionando la superficie n'estudiu, con trazos verticales, de tal manera que vamos llogrando pequeños rectángulos, y amenorgando cada vez más l'anchu de los rectángulos emplegaos pa faer l'aproximamientu, va llograse un meyor resultáu. Por casu, estrememos l'intervalu en cinco partes, emplegando los puntos 0, ¹⁄₅, ²⁄₅,³⁄₅,⁴⁄₅ y finalmente l'ascisa 1. Llógrense cinco rectángulos que les sos altores determinar aplicando la función coles ascises enantes descrites (del llau derechu de cada cachu de la curva), asina ${\sqrt {{}^{1}/_{5}}}$, ${\sqrt {{}^{2}/_{5}}}$, ${\sqrt {{}^{3}/_{5}}}$… y asina hasta ${\sqrt {1}}=1\,$. Sumando les árees d'estos rectángulos, llógrase un segundu aproximamientu de la integral que se ta buscando,

${\sqrt {\frac {1}{5}}}\left({\frac {1}{5}}-0\right)+{\sqrt {\frac {2}{5}}}\left({\frac {2}{5}}-{\frac {1}{5}}\right)+\ldots +{\sqrt {\frac {5}{5}}}\left({\frac {5}{5}}-{\frac {4}{5}}\right)\approx 0,7497\,\!$

Nótese que se ta sumando una cantidá finita de valores de la función f, multiplicaos pola diferencia ente dos puntos d'aproximamientu socesivos. Puede vese fácilmente que los continuos aproximamientos siguen dando un valor más grande que'l de la integral. Emplegando más pasos llógrase una aproximamientu más afechu, pero nun va ser nunca exacta. Si en cuenta de 5 subintervalos tómense dolce y agora tomamos les ascises de la esquierda, tal como s'amuesa nel dibuxu, llógrase un envaloráu pa l'área, de 0,6203, que nesti casu ye de menor valor que l'enantes determináu. Escurrir clave ye la transición dende la suma de una cantidá finita de diferencies de puntos d'aproximamientu multiplicaos polos respeutivos valor de la función, hasta usar pasos infinitamente finos, o infinitesimales. La notación

$\int f(x)\,{\text{d}}x\,\!$

concibe la integral como una suma ponderada (denotada pola "S" allargada), de los valores de la función multiplicaos por pasos d'anchor infinitesimal, los llamaos diferenciales (indicaos por dx).

Con respectu al cálculu real d'integrales, el teorema fundamental del cálculu, por cuenta de Newton y Leibniz, ye'l venceyu fundamental ente les operaciones de derivación ya integración. Aplicándolo al curvu raigañu cuadráu, tiense que mirar la función rellacionada $F(x)={\frac {2}{3}}x^{\frac {3}{2}}$ y a cencielles tomar $F(1)-F(0)\,$, onde $0\,$ y $1\,$ son les fronteres del intervalu [0,1]. Ésti ye un exemplu d'una regla xeneral, que diz que pa $f(x)=x^{q}$, con q ≠ −1, la función rellacionada, la llamada primitiva, ye $F(x)={\frac {x^{q+1}}{q+1}}$. D'esta miente, el valor exactu del área so la curva calcúlase formalmente como:

$\int _{0}^{1}{\sqrt {x}}\,dx=\int _{0}^{1}x^{\frac {1}{2}}\,{\text{d}}x=\left.({\frac {2}{3}}x^{\frac {3}{2}})\right|_{0}^{1}={\frac {2}{3}}1^{\frac {3}{2}}-{\frac {2}{3}}0^{\frac {3}{2}}={\frac {2}{3}}.$

Como puede vese, el segundu aproximamientu de 0,7 (con cinco rectangulitos), refundió un valor cimeru al valor exactu; sicasí l'aproximamientu con 12 rectangulitos de 0,6203 ye una estimación bien per debaxo del valor exactu (que ye de 0,666...).

Históricamente, dempués de que los primeros esfuercios de definir rigorosamente los infinitesimales non fructificasen, Riemann definió formalmente les integrales como'l Llende d'una función llende de sumes ponderaes, de forma que el dx suxer la llende d'una diferencia (l'anchor del intervalu). La dependencia de la definición de Riemann de los intervalos y la continuidá motivó l'apaición de nueves definiciones, especialmente la integral de Lebesgue, que se basa na habilidá d'estender la idea de "midida" de maneres muncho más flexibles. Asina, la notación

$\int _{A}f(x)\,{\text{d}}\mu \,\!$

fai referencia a una suma ponderada de valores en que s'estrema la función, onde μ mide'l pesu que se tien qu'asignar a cada valor. (Equí A indica la rexón d'integración.) La xeometría diferencial, cola so "cálculu de variedaes", apurre otra interpretación a esta notación familiar. Agora f(x) y dx pasen a ser una forma diferencial, ω = f(x)dx, apaez un nuevu operador diferencial d, conocíu como la derivada esterior, y el teorema fundamental pasa a ser el (más xeneral) teorema de Stokes,

$\int _{A}\mathbf {d} \omega =\int _{\partial A}\omega ,\,\!$

a partir del cual derívase'l teorema de Green, el teorema de la diverxencia, y el teorema fundamental del cálculu.

Apocayá, los infinitesimales remanecieron con rigor, al traviés d'innovaciones modernes como'l analís non estándar. Estos métodos non solo reivindiquen la intuición de los pioneros, tamién lleven escontra les nueves matemátiques, y faen más intuitivu y comprensible el trabayu con cálculu infinitesimal.

A pesar de qu'hai diferencies ente toes estes concepciones de la integral, hai un solapamiento considerable. Asina, l'área de la piscina oval puede topase como una elipse xeométrica, como una suma d'infinitesimales, como una integral de Riemann, como una integral de Lebesgue, o como una variedá con una forma diferencial. La resultancia llograda col cálculu va ser el mesmu en tolos casos.

Definiciones formales

Hai munches maneres de definir formalmente una integral, non toes equivalentes. Establécense diferencies pa poder encetar casos especiales que nun pueden ser integrables con otres definiciones, pero tamién n'ocasiones por razones pedagóxiques. Les definiciones más utilizaes de la integral son les integrales de Riemann y les integrales de Lebesgue.

Integral de Riemann

Artículu principal: Integral de Riemann

Integral col planteamientu de Riemann fai una suma basada nuna partición etiquetada, con posiciones de muestreo y anchores irregulares (el máximu en colloráu). El verdaderu valor ye 3,76; la estimación llograda ye 3,648.

La integral de Riemann definir en términos de sumas de Riemann de funciones respeuto de particiones etiquetaes d'un intervalu. Sía [a,b] un intervalu zarráu de la recta real; entós una partición etiquetada de [a,b] ye una secuencia finita

$a=x_{0}\leq t_{1}\leq x_{1}\leq t_{2}\leq x_{2}\leq \cdots \leq x_{n-1}\leq t_{n}\leq x_{n}=b.\,\!$ y denotamos la partición como ${\mathit {P}}=\{x_{i}|i=0,1,...,n\}\,\!$

Converxencia de sumatorios de Riemann a midida en que se parten los intervalos, cuando se muestrea a ■ la derecha, ■ el mínimu, ■ el máximu, o ■ la esquierda.

Esto estrema al intervalu [a,b] en n subintervalos [x_i−1, x_i], cada unu de los cualos ye "etiquetáu" con un puntu especificáu t_i de; [x_i−1, x_i]. Sía Δ_i = x_i−x_i−1 l'anchor del subintervalo i; el pasu d'esta partición etiquetada ye l'anchu del subintervalo más grande llográu pola partición, max_i=1…n Δ_i. Un sumatorio de Riemann d'una función f respectu d'esta partición etiquetada defínese como :$\sum _{i=1}^{n}f(t_{i})\Delta _{i};$ Asina cada términu del sumatorio ye l'área del rectángulu con altor igual al valor de la función nel puntu especificáu del subintervalo dau, y del mesmu anchor que l'anchor del subintervalo. La integral de Riemann d'una función f sobre l'intervalu [a,b] ye igual a S si:

Pa tou ε > 0 esisti δ > 0 tal que, pa cualquier partición etiquetada [a,b] con pasu más pequeñu que δ, tiense ::$\left|S-\sum _{i=1}^{n}f(t_{i})\Delta _{i}\right|<\varepsilon$, onde $S=\int _{a}^{b}f=\lim _{\|{\Delta _{i}}\|\to 0}\sum _{i=1}^{n}f(t_{i})\Delta _{i}$

Cuando les etiquetes escoyíes dan el máximu (o mínimu) valor de cada intervalu, el sumatorio de Riemann pasa a ser un sumatorio de Darboux cimeru (o inferior), lo que suxer la estrecha conexón qu'hai ente la integral de Riemann y la integral de Darboux.

Integral de Darboux

Artículu principal: Integral de Darboux

La Integral de Darboux definir en términos de sumes de los siguientes tipos:

$L({\mathit {f}},P)=\sum _{i}^{n}m_{i}(x_{i}-x_{i-1}),\qquad O({\mathit {f}},P)=\sum _{i}^{n}M_{i}(x_{i}-x_{i-1})$

Llamaes suma inferior y cimeru respeutivamente, onde:

$M_{i}=\sup\{f(x)|x\in [x_{i-1},x_{i}]\},\qquad m_{i}=\inf\{f(x)|x\in [x_{i-1},x_{i}]\}$

son los altores de los rectángulos, y x_i-x_i-1 el llargor de la base de los rectángulos. La integral de Darboux ta definida como l'únicu númberu acutáu ente les sumes inferior y superior, esto ye,

$L(f,P)\leq \int _{a}^{b}f\leq O(f,P)$

La interpretación xeométrica de la integral de Darboux sería'l cálculu del área de la rexón en [a,b] pol Métodu refechu. La integral de Darboux d'una función f en [a,b] esiste si y solu si

$\sup \left\lbrace L(f,P)\right\rbrace =\inf \left\lbrace O(f,P)\right\rbrace$

Del Teorema de Carauterización que diz que si f ye integrable en [a,b] entós ∀ε>0 ∃ P partición de [a,b] : 0≤O(f,P)-L(f,P)≤ε, evidencia la equivalencia ente les definiciones d'Integral de Riemman ya Integral de Darboux pos se sigue que

$\int _{a}^{b}f-\sum _{i=1}^{n}f(t_{i})\Delta _{i}\leq O(f,P)-L(f,P)\leq \varepsilon$.

Integral de Lebesgue

Artículu principal: Integral de Lebesgue

Integración de Riemann-Darboux (azul) ya integración de Lebesgue (colloráu).

La integral de Riemann nun ta definida pa un anchu abanicu de funciones y situaciones d'importancia práutica (y d'interés teóricu). Por casu, la integral de Riemann puede integrar fácilmente la densidá pa llograr la masa d'una viga d'aceru, pero nun puede afaese a una bola d'aceru que se sofita enriba. Esto motiva la creación d'otres definiciones, so les cualos puede integrase un surtíu más ampliu de funciones. La integral de Lebesguesobremanera, llogra una gran flexibilidá a base de centrar l'atención nos pesos de la suma ponderada.

Asina, la definición de la integral de Lebesgue empieza con una midida, μ. Nel casu más senciellu, la midida de Lebesgue μ(A) d'un intervalu A = [a, b] ye'l so anchu, b − a, asina la integral de Lebesgue coincide cola integral de Riemann cuando esisten dambes. En casos más complicaos, los conxuntos a midir pueden tar altamente estazaos, ensin continuidá y ensin nenguna paecencia a intervalos.

Pa esplotar esta flexibilidá, la integral de Lebesgue invierte l'enfoque de la suma ponderada. Como espresa Folland: "Pa calcular la integral de Riemann de f, se particiona el dominiu [a, b] en subintervalos", ente que na integral de Lebesgue, "de fechu lo que se ta particionando ye'l percorríu de f".

Un enfoque habitual define primero la integral de la función carauterística d'un Teoría de la midida conxuntu medible A por:

$\int 1_{A}d\mu =\mu (A)$.

Esto estiéndese por linealidad a les funciones gradiaes simples, que solo tienen un númberu finito n, de valores distintos non negativos:

${\begin{aligned}\int s\,d\mu &{}=\int \left(\sum _{i=1}^{n}a_{i}1_{A_{i}}\right)d\mu \\&{}=\sum _{i=1}^{n}a_{i}\int 1_{A_{i}}\,d\mu \\&{}=\sum _{i=1}^{n}a_{i}\,\mu (A_{i})\end{aligned}}$

(onde la imaxe de A_i al aplica-y la función gradiada s ye'l valor constante a_i). Asina, si Y ye un conxuntu medible, defínese :$\int _{Y}s\,d\mu =\sum _{i=1}^{n}a_{i}\,\mu (A_{i}\cap Y).$ Entós, pa cualesquier función medible non negativa f defínese :$\int _{Y}f\,d\mu =\sup \left\{\int _{Y}s\,d\mu \,\colon 0\leq s\leq f{\text{ y }}s{\text{ye una funcion gradiada}}\right\};$ Esto ye, establezse que la integral de f ye'l supremu de toles integrales de funciones gradiaes que son más pequeñes o iguales que f. Una función medible cualesquier f, dixebrar ente los sos valores positivos y negativos a base de definir

${\begin{aligned}f^{+}(x)&{}={\begin{cases}f(x),&{\text{si }}f(x)>0\\0,&{\text{d'otra miente}}\end{cases}}\\f^{-}(x)&{}={\begin{cases}-f(x),&{\text{si }}f(x)<0\\0,&{\text{d'otra miente}}\end{cases}}\end{aligned}}$

Finalmente, f ye Lebesgue integrable si :$\int _{Y}|f|\,d\mu <\infty ,\,\!$ y entós defínese la integral por

$\int _{Y}f\,d\mu =\int _{Y}f^{+}\,d\mu -\int _{Y}f^{-}\,d\mu .\,\!$

Cuando l'espaciu métricu nel que tán definíes les funciones ye tamién un espaciu topolóxicu llocalmente compactu (como ye'l casu de los númberos reales R), les midíes compatibles cola topoloxía nun sentíu fayadizu (midíes de Radon, de les cualos ye un exemplu la midida de Lebesgue) una integral respectu d'elles puédese definir d'otra manera, empezar a partir de les integrales de les funciones continues con soporte compactu. De forma más precisa, les funciones compactamente soportaes formen un espaciu vectorial que porta una topoloxía natural, y puede definise una midida (Radon) como cualesquier funcional llinial continuu d'esti espaciu; entós el valor d'una midida nuna función compactamente soportada, ye tamién, por definición, la integral de la función. Entós síguese espandiendo la midida (la integral) a funciones más xenerales por continuidá, y defínese la midida d'un conxuntu como la integral de la so función carauterística. Este ye l'enfoque que toma Bourbaki y ciertu númberu d'otros autores. Pa más detalles, vease midíes de Radon.

Otres integrales

A pesar de que les integrales de Riemann y Lebesgue son les definiciones más importantes d'integral, hai unes cuántes más, por casu:

• La integral de Riemann-Stieltjes, una estensión de la integral de Riemann.
• La integral de Lebesgue-Stieltjes, desenvuelta por Johann Radon, que xeneraliza les integrales de Riemann-Stieltjes y de Lebesgue.
• La integral de Daniell, qu'inclúi la integral de Lebesgue y la integral de Lebesgue-Stieltjes ensin tener que depender de nenguna midida.
• La integral de Henstock-Kurzweil, definida de forma variada por Arnaud Denjoy, Oskar Perron, y Jaroslav Kurzweil, y desenvuelta por Ralph Henstock.
• La integral de Haar, que ye la integral de Lebesgue cola midida de Haar.
• La integral de McShane.
• La integral de Bochner.
• La integral de Itō, integral qu'estiende a la integral de Riemann-Stieltjes, dexa integrar al respeutive de procesos estocásticos que pueden nun ser de variación acutada como'l movimientu browniano.

Propiedaes de la integración

Linealidad

• El conxuntu de les funciones Riemann integrables nun intervalu zarráu [a, b] formen un espaciu vectorial coles operaciones de suma (la función suma d'otros dos ye la función qu'a cada puntu fai-y corresponder la suma de les imáxenes d'esti puntu por caúna de les otres dos) y la multiplicación por un angular. La operación integración

$f\mapsto \int _{a}^{b}f\;dx$

ye un funcional llinial d'esti espaciu vectorial. Asina, de primeres, el conxuntu de funciones integrables ye cerráu cola combinación llinial, y de segundes, la integral d'una combinación llinial ye la combinación llinial de les integrales,

$\int _{a}^{b}(\alpha f+\beta g)(x)\,dx=\alpha \int _{a}^{b}f(x)\,dx+\beta \int _{a}^{b}g(x)\,dx.\,$

• De forma asemeyada, el conxuntu de les funciones reales Lebesgue integrables nun espaciu métricu Y dadu, cola midida μ ye zarráu respectu de les combinaciones lliniales y polo tanto formen un espaciu vectorial, y l'integral de Lebesgue

$f\mapsto \int _{Y}fd\mu$

ye un funcional llinial d'esti espaciu vectorial, de forma que

$\int _{Y}(\alpha f+\beta g)\,d\mu =\alpha \int _{Y}f\,d\mu +\beta \int _{Y}g\,d\mu .$

• De forma más xeneral, si toma l'espaciu vectorial de toles funciones medibles sobre un espaciu métricu (Y,μ), que tomen valores nun espaciu vectorial topolóxicu completu llocalmente compactu V sobre un campu topolóxico llocalmente compactu K, f : Y → V. Entós puede definise una aplicación integración astracta qu'a cada función f asígna-y un elementu de V o'l símbolu ∞, ::$f\mapsto \int _{Y}fd\mu ,\,$

que ye compatible coles combinaciones lliniales. Nesta situación, la linealidad sostener pal subespacio de les funciones, que la so integral ye un elementu de V (esto ye, les integrales "finitas"). Los casos más importantes surden cuando K ye R, C, o una estensión finita del campu Qp de númberos p-ádicos, y V ye un espaciu vectorial de dimensión finita sobre K, y cuando K=C y V ye un espaciu de Hilbert complexu.

La linealidad, xunto con delles propiedá naturales de continuidá y la normalización pa ciertes clases de funciones "simples", pueden usase pa dar una definición alternativa d'integral. Este ye l'enfoque de Daniell pal casu de funciones reales nun conxuntu X, xeneralizáu por Bourbaki a funciones que tomen valores nun espaciu vectorial topológicamente compactu. Vease Hildebrandt (1953) pa una carauterización axomática de la integral.

Desigualdaes con integrales

Verifíquense delles desigualdaes xenerales para funciones Riemann integrables definíes nun intervalu zarráu y acutáu [a, b] y pueden xeneralizase a otres nociones d'integral (Lebesgue y Daniell).

• Cotes cimeres ya inferiores. Una función f integrable en [a, b], ye necesariamente acutada nel intervalu. Polo tanto hai dos númberos reales m y M tales que m ≤ f (x) ≤ M pa tou x de [a, b]. Puesto que los sumatorios cimeru ya inferior de f sobre [a, b] son tamién acutaos pa m(b − a) y M(b − a) respeutivamente, d'equí resulta que ::

$m(b-a)\leq \int _{a}^{b}f(x)\,dx\leq M(b-a).$

• Desigualdaes ente funciones. Si f(x) ≤ g(x) pa tou x de [a, b] entós cada unu de los sumatorios cimeru ya inferior de f son acutaos inferior y superiormente polos sumatorios cimeru ya inferior de g respeutivamente. Asina ::

$\int _{a}^{b}f(x)\,dx\leq \int _{a}^{b}g(x)\,dx.$

Esto ye una xeneralización de les desigualdaes anteriores, yá que M '(b − a) ye la integral de la función constante con valor M nel intervalu [a, b].

• Subintervalos. Si [c, d] ye un subintervalo de [a, b] y f(x) ye non negativa pa tou x, entós ::

$\int _{c}^{d}f(x)\,dx\leq \int _{a}^{b}f(x)\,dx.$

• Productos y valores absolutos de funciones. Si f y g son dos funciones, entós podemos emplegar el so productu, potencies y valores absolutos:

$(fg)(x)=f(x)g(x),\;f^{2}(x)=(f(x))^{2},\;|f|(x)=|f(x)|.\,$

Si f ye Riemann integrable en [a, b] entós lo mesmo cumplir pa |f|, y ::

$\left|\int _{a}^{b}f(x)\,dx\right|\leq \int _{a}^{b}|f(x)|\,dx.$

Ye más, si f y g son dambes Riemann integrables entós f ², g ², y fg son tamién Riemann integrables, y ::

$\left(\int _{a}^{b}(fg)(x)\,dx\right)^{2}\leq \left(\int _{a}^{b}f(x)^{2}\,dx\right)\left(\int _{a}^{b}g(x)^{2}\,dx\right).$

Esta desigualdá conozse como desigualdá de Cauchy-Schwarz, y desempeña un papel fundamental na teoría de los espacios de Hilbert, onde'l llau de la derecha interprétase como'l productu angular de dos funciones integrables f y g nel intervalu [a, b].

• Desigualdá de Hölder. Si p y q son dos númberos reales, 1 ≤ p, q ≤ ∞ con 1/p + 1/q = 1, y f y g son dos funciones Riemann integrables. Entós les funciones |f|^p y |g|^q tamién son integrables y cumplir la desigualdá de Hölder:

$\left|\int f(x)g(x)\,dx\right|\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}\left(\int \left|g(x)\right|^{q}\,dx\right)^{1/q}.$

Pal casu de p = q = 2, la desigualdá de Hölder pasa a ser la desigualdá de Cauchy–Schwarz.

• Desigualdá de Minkowski. Si p ≥ 1 ye un númberu real y f y g son funciones Riemann integrables. Entós |f|^p, |g|^p y |f + g|^p son tamién Riemann integrables y cumplir la desigualdá de Minkowski:

$\left(\int \left|f(x)+g(x)\right|^{p}\,dx\right)^{1/p}\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}+\left(\int \left|g(x)\right|^{p}\,dx\right)^{1/p}.$

Una desigualdá análoga a ésta pa la integral de Lebesgue usar na construcción de los espacios L^p.

Convenciones

Nesta seición f ye una función real Riemann integrable. La integral

$\int _{a}^{b}f(x)\,dx$

sobre un intervalu [a, b] ta definida si a < b. Esto significa que los sumatorios cimeros ya inferiores de la función f evalúense sobre una partición a = x₀ ≤ x₁ ≤ . . . ≤ x_n = b que los sos valores x_i son crecientes. Geométricamente significa que la integración tien llugar "d'esquierda a derecha", evaluando f dientro d'intervalos [x_i , x_i +1] onde l'intervalu con un índiz más grande queda a la derecha del intervalu con un índiz más pequeñu. Los valores a y b, los puntos estremos del intervalu, denominar llendes d'integración de f. Les integrales tamién pueden definise si a > b:

• Inversión de les llendes d'integración. si a > b entós defínese ::

$\int _{a}^{b}f(x)\,dx=-\int _{b}^{a}f(x)\,dx.$ Ello, con a = b, implica:

• Integrales sobre intervalos de longitud cero. si a ye un númberu real entós ::

$\int _{a}^{a}f(x)\,dx=0.$

La primer convención ye necesaria al calcular integrales sobre subintervalos de [a, b]; la segunda diz qu'una integral sobre un intervalu dexeneráu, o un puntu, tien que ser cero. Un motivu pa la primer convención ye que la integrabilidad de f sobre un intervalu [a, b] implica que f ye integrable sobre cualesquier subintervalo [c, d], pero en particular les integrales tienen la propiedá de que:

• Aditividad de la integración sobre intervalos. si c ye cualesquier elementu de [a, b], entós ::

$\int _{a}^{b}f(x)\,dx=\int _{a}^{c}f(x)\,dx+\int _{c}^{b}f(x)\,dx.$ Cola primer convención la rellación resultante : ${\begin{aligned}\int _{a}^{c}f(x)\,dx&{}=\int _{a}^{b}f(x)\,dx-\int _{c}^{b}f(x)\,dx\\&{}=\int _{a}^{b}f(x)\,dx+\int _{b}^{c}f(x)\,dx\end{aligned}}$ queda bien definida pa cualesquier permutación cíclica de a, b, y c.

En llugar de ver lo anterior como convenciones, tamién puede adoptase el puntu de vista de que la integración faise solu sobre variedaes empobinaes. Si M ye una tal forma m-dimensional empobinada, y M' ye la mesma forma con orientación opuesta y ω ye una m-forma, entós tiense (vease más embaxo la integración de formes diferenciales):

$\int _{M}\omega =-\int _{M'}\omega \,.$

Teorema fundamental del cálculu

Artículu principal: Teorema fundamental del cálculu

El teorema fundamental del cálculu ye l'afirmación de que la derivación y l'integración son operaciones inverses: si una función continua primero intégrase y depués derívase, recupérase la función orixinal. Una consecuencia importante, n'ocasiones denomada'l segundu teorema fundamental del cálculu, dexa calcular integrales a base d'emplegar una primitiva de la función a integrar.

Enunciáu de los teoremas

• Teorema fundamental del cálculu. Sía f una función real integrable definida nun intervalu zarráu [a, b]. Si defínese F pa cada x de [a, b] por

$F(x)=\int _{a}^{x}f(x)\,dx.$

entós F ye continua en [a, b]. Si f ye continua en x de [a, b], entós F ye derivable en x, y F ′(x) = f(x).

• Segundu teorema fundamental del cálculu. Sía f una función real, integrable definida nun intervalu zarráu [a, b]. Si F ye una función tal que F ′(x) = f(x) pa tou x de [a, b] (esto ye, F ye una primitiva de f), entós ::$\int _{a}^{b}f(x)\,dx=F(b)-F(a).$

• Corolariu. Si f ye una función continua en [a, b], entós f ye integrable en [a, b], y F, definida por

$F(x)=\int _{a}^{b}f(x)\,dx$

ye una primitiva de f en [a, b]. Amás, ::$\int _{a}^{b}f(x)\,dx=F(b)-F(a).$

Estensiones

Integrales impropies

Artículu principal: Integral impropia

La integral impropia
$\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi$
tien intervalu ensin acutar tantu nel dominiu como nel percorríu.

Una integral de Riemann "mesma" supón que l'integrando ta definíu y ye finito nun intervalu zarrao y acutao, que los sos estremos son les llendes d'integración. Una integral impropia apaez cuando una o más d'estes condiciones nun se satisfai. En dellos casos, estes integrales pueden definise tomando'l Llende d'una función llende d'una socesión d'integrales de Riemann propies sobre intervalos socesivamente más llargos.

Si l'intervalu nun ye acutáu, por casu nel so estremu cimeru, entós la integral impropia ye la llende cuando'l puntu final tiende a infinitu.

$\int _{a}^{\infty }f(x)dx=\lim _{b\to \infty }\int _{a}^{b}f(x)dx$

Si l'integrando solo ta definíu nun intervalu finito semiabierto, por casu (a,b], entós, otra vegada la llende puede suministrar un resultáu finito.

$\int _{a}^{b}f(x)dx=\lim _{\epsilon \to 0}\int _{a+\epsilon }^{b}f(x)dx$

Esto ye, la integral impropia ye'l Llende d'una función llende d'integrales propies cuando unu de los puntos estremos del intervalu d'integración avérase, yá seya a un númberu real especificáu, o ∞, o −∞. En casos más complicaos, faen falta llendes nos dos puntos estremos o en puntos interiores.

Por casu, la función ${\tfrac {1}{(x+1){\sqrt {x}}}}$ integrada dende 0 a ∞ (imaxe de la derecha). Nel estremu inferior, a midida que x averar a 0 la función tiende a ∞, y l'estremu cimeru ye él mesmu ∞, a pesar de que la función tiende a 0. Asina, esta ye una integral doblemente impropia. Integrada, por casu, dende 1 hasta 3, con un sumatorio de Riemann ye abondu pa llograr un resultáu de ${\tfrac {\pi }{6}}$. Pa integrar dende 1 hasta ∞, un sumatorio de Riemann nun ye posible. Agora bien, cualquier llende cimera finito, por casu t (con t > 1), da un resultáu bien definíu, ${\tfrac {\pi }{2}}-2\arctan {\tfrac {1}{\sqrt {t}}}$. Esta resultancia tien una llende finito cuando t tiende a infinitu, que ye ${\tfrac {\pi }{2}}$. De forma asemeyada, la integral dende ¹⁄₃ hasta a 1 almite tamién un sumatorio de Riemann, que por casualidá da de nuevu ${\tfrac {\pi }{6}}$. Sustituyendo ¹⁄₃ por un valor positivu arbitrariu s (con s < 1) resulta igualmente un resultáu definida y da $-{\tfrac {\pi }{2}}+2\arctan {\tfrac {1}{\sqrt {s}}}$. Ésti, tamién tien una llende finito cuando s tiende a cero, que ye ${\tfrac {\pi }{2}}$. Combinando les llendes de los dos fragmentos, la resultancia d'esta integral impropia ye :${\begin{aligned}\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}&{}=\lim _{s\to 0}\int _{s}^{1}{\frac {dx}{(x+1){\sqrt {x}}}}+\lim _{t\to \infty }\int _{1}^{t}{\frac {dx}{(x+1){\sqrt {x}}}}\\&{}=\lim _{s\to 0}\left(-{\frac {\pi }{2}}+2\arctan {\frac {1}{\sqrt {s}}}\right)+\lim _{t\to \infty }\left({\frac {\pi }{2}}-2\arctan {\frac {1}{\sqrt {t}}}\right)\\&{}={\frac {\pi }{2}}+{\frac {\pi }{2}}\\&{}=\pi .\end{aligned}}$ Esti procesu nun tien l'ésitu garantizáu; una llende puede nun esistir, o puede ser infinitu. Por casu, sobre l'intervalu zarráu de 0 a 1 la integral de ${\tfrac {1}{x^{2}}}$ nun converxe; y sobre l'intervalu abiertu del 1 a ∞ la integral de ${\tfrac {1}{\sqrt {x}}}$ nun converxe.

La integral impropia
$\int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}=6$
nun ta acutada internamente, pero ambos llendes (pela derecha y pela esquierda) esisten.

Tamién puede pasar qu'un integrando nun tea acutáu nun puntu interior, nesti casu la integral haber de partir nesti puntu, y la llende de les integrales de los dos llaos han d'esistir y han de ser acutaos. Asina :${\begin{aligned}\int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}&{}=\lim _{s\to 0}\int _{-1}^{-s}{\frac {dx}{\sqrt[{3}]{x^{2}}}}+\lim _{t\to 0}\int _{t}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}\\&{}=\lim _{s\to 0}3(1-{\sqrt[{3}]{s}})+\lim _{t\to 0}3(1-{\sqrt[{3}]{t}})\\&{}=3+3\\&{}=6.\end{aligned}}$ A la integral similar

$\int _{-1}^{1}{\frac {dx}{x}}\,\!$

nun se-y puede asignar un valor d'esta forma, yá que les integrales percima y per debaxo de cero nun converxen independientemente (sicasí, vease valor principal de Cauchy.)

Integración múltiple

Artículu principal: Integral múltiple

Integral doble como'l volume llindáu por una superficie.

Les integrales pueden calculase sobre región distintes de los intervalos. Polo xeneral, una integral sobre un conxuntu Y d'una función f escríbese:

$\int _{Y}f(x)\,dx.$

Equí x nun fai falta que seya necesariamente un númberu real, sinón que puede ser cualesquier otra cantidá apropiada, por casu, un vector de R3. El teorema de Fubini demuestra qu'estes integrales pueden reescribise como una integral iterada. N'otres pallabres, la integral puede calculase a base d'integrar les coordenaes una por una.

De la mesma manera que la integral definida d'una función positiva representa'l área de la rexón zarrada ente la gráfica de la función y la exa x, la integral doble d'una función positiva de dos variables representa'l volume de la rexón entendida ente la superficie definida pola función y el planu que contién el so dominio. (El mesmu volume puede llograse al traviés d'una integral triple — la integral de la función de trés variables — de la función constante f(x, y, z) = 1 sobre la rexón mentada antes ente la superficie y el planu, lo mesmo puede faese con una integral doble pa calcular una superficie.) Si'l númberu de variables ye mayor, entós la integral representa un hipervolumen, el volume d'un sólidu de más de tres dimensiones que nun se puede representar gráficamente.

Por casu, el volume del paralelepípedu de cares 4 × 6 × 5 puede llograse de dos maneres:

• Cola integral doble ::

$\iint _{D}5\ dx\,dy$

de la función f(x, y) = 5 calculada na rexón D del planu xy que ye la base del paralelepípedu.

• Cola integral triple ::$\iiint _{\mathrm {paralelepipedo} }1\,dx\,dy\,dz$

de la función constante 1 calculada sobre'l mesmu paralelepípedu (a pesar de qu'esti segundu métodu tamién puede interpretase como'l hipervolumen d'un hiperparalelepípedo de cuatro dimensiones que tien como base'l paralelepípedu en cuestión y un altor constante de 1, como l'altor ye 1 el volume coincide cola área de la base).

Puesto que ye imposible calcular la antiderivada d'una función de más d'una variable, nun esisten les integrales múltiples indefiníes: tales integrales son toes definíes.

Integrales de llinia

Artículu principal: Integral de llinia

Una integral de llinia atropa elementos a lo llargo d'una curva.

El conceutu d'integral puede estendese a dominios d'integración más xenerales, tales como les llinies curves y les superficies. Estes integrales conócense como integrales de llinia ya integrales de superficie respeutivamente. Tienen importantes aplicaciones na física cuando se trata con campos vectoriales.

Una integral de llinia ye una integral onde la función a integrar ye evaluada a lo llargo d'una curva. Utilícense delles integrales curvillinies distintes. Nel casu d'una curva zarrada tamién-y la denomina integral de contorna.

La función a integrar puede ser un campu angular o un campu vectorial. El valor de la integral curvillinia ye la suma de los valores del campu nos puntos de la llinia, sopesaos por dalguna función angular de la curva (davezu la longitud del arcu o, nel casu d'un campu vectorial, el productu angular del campu vectorial por un vector diferencial de la curva). Esta ponderación estrema les integrales curvillinies de les integrales más sencielles definíes sobre intervalos.

Munches fórmules sencielles de la física tienen de forma natural análogues continues en términos d'integrales de llinia; por casu, el fechu de que'l trabayu seya igual a la fuercia multiplicada pola distancia puede espresase (en términos de cantidaes vectoriales) como:

$W={\vec {F}}\cdot {\vec {d}}$

que tien el so paralelismu na integral de llinia :$W=\int _{C}{\vec {F}}\cdot d{\vec {s}}$ qu'atropa los componentes vectoriales a lo llargo d'un camín continuu, y asina calcula'l trabayu realizáu por un oxetu al movese al traviés d'un campu, como por casu un campu llétrico o un campu gravitatorio.

Integrales de superficie

Artículu principal: Integral de superficie

La definición de les integrales de superficie fuelga na división de la superficie en pequeños elementos de superficie.

Una integral de superficie ye una integral definida calculada sobre una superficie (que puede ser un conxuntu curvado nel espaciu; puede entendese como la integral doble análoga a la integral de llinia. La función a integrar puede ser un campu angular o un campu vectorial. El valor de la integral de superficie ye la suma ponderada de los valores del campu en tolos puntos de la superficie. Esto puédese consiguir a base d'estremar la superficie n'elementos de superficie, que apurren la partición pa los sumatorios de Riemann.

Como exemplu de les aplicaciones de les integrales de superficie, puede considerase un campu vectorial v sobre una superficie S; esto ye, pa cada puntu x de S, v(x) ye un vector. Imaxínese que se tien un fluyíu fluyendo al traviés de S, de forma que v(x) determina la velocidá del fluyíu nel puntu x. El caudal defínese como la cantidá de fluyíu que flúi al traviés de S na unidá de tiempu. Pa topar el caudal, hai que calcular el productu angular de v pol vector unitariu normal a la superficie S en cada puntu, lo que nos dará un campu angular, qu'integramos sobre la superficie:

$\int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }$.

El caudal de fluyíu d'esti exemplu puede ser d'un fluyíu físicu como l'agua o l'aire, o d'un fluxu llétrico o magnéticu. Asina, les integrales de superficie tienen aplicaciones na físiquesobremanera na teoría clásica del electromagnetismu.

Integrales de formes diferenciales

Artículu principal: Forma diferencial

Una forma diferencial ye un conceutu matemáticu nos campos del cálculu multivariable, topoloxía diferencial y tensores. La notación moderna de les formes diferenciales, según la idea de les formes diferenciales como'l productu esterior de derivaes esteriores formando un álxebra esterior, foi presentada por Élie Cartan.

Empieza trabayándose nun conxuntu abiertu de Rⁿ. Una 0-forma defínese como una función infinitamente derivable f. Cuando s'integra una función f sobre un subespacio de m-dimensional S de Rⁿ, escríbese como :$\int _{S}f\,dx^{1}\cdots dx^{m}.$ (Los superíndices nun son esponentes.) Puede considerase que dx¹ hasta dxⁿ son oxetos formales ellos mesmos, más qu'etiquetes añadíes pa faer que la integral asemeyar a los sumatorios de Riemann. De forma alternativa pueden vese como covectores, y polo tanto como una midida de la "densidá" (integrable nun sentíu xeneral). A dx¹, …,dxⁿ denominar 1-formas básiques.

Defínese'l conxuntu de toos estos productos como les 2-formes básiques, y de forma similar defínese'l conxuntu de los productos de la forma dx^a∧dx^b∧dx^c como les 3-formes básiques. Una k-forma xeneral ye polo tanto una suma ponderada de k-formes básiques, onde los pesos son les funciones infinitamente derivables f. Toes xuntes formen un espaciu vectorial, siendo les k-formes básiques los vectores base, y les 0-formes (funciones infinitamente derivables) el campu d'angulares. El productu esterior estender a les k-formes de la forma natural. Sobre Rⁿ a lo más n covectores pueden ser linealmente independientes, y asina una k-forma con k > n va ser siempres cero pola propiedá alternante.

Amás del productu esterior, tamién esiste l'operador derivada esterior d. Esti operador fai corresponder a les k-formes (k+1)-formes. Pa una k-forma ω = f dx^a sobre Rⁿ, defínese l'acción de d por:

${\mathbf {d} }{\omega }=\sum _{i=1}^{n}{\frac {\partial f}{\partial x_{i}}}dx^{i}\wedge dx^{a}.$

con estensión a les k-formes xenerales que se dan linealmente.

Esti planteamientu más xeneral dexa un enfoque de la integración sobre variedaes llibre de coordenaes. Tamién dexa una xeneralización natural del teorema fundamental del cálculu, denomada teorema de Stokes, que puede establecese como

$\int _{\Omega }{\mathbf {d} }\omega =\int _{\partial \Omega }\omega \,\!$

onde ω ye una k-forma xeneral, y ∂Ω indica la frontera de la rexón Ω. Asina nel supuestu de que ω seya una 0-forma y Ω seya un intervalu zarráu de la recta real, el teorema de Stokes amenorgar al teorema fundamental del cálculu. Nel casu de que ω seya una 1-forma y Ω seya una rexón de dimensión 2 nel planu, el teorema amenorgar al teorema de Green. De manera similar, emplegando 2-formes, 3-formes y la dualidá de Hodge, puede llegase al teorema de Stokes y al teorema de la diverxencia. D'esta forma puede trate que les formes diferenciales suministren una potente visión unificadora de la integración.

Métodos y aplicaciones

Cálculu d'integrales

Artículu principal: Métodos d'integración

La téunica más básica pa calcular integrales d'una variable real basar nel teorema fundamental del cálculu. Venir# de la siguiente forma:

1. Escuéyese una función f(x) y un intervalu [a, b].
2. Tópase una antiderivada de f, esto ye, una función F tal que F' = f.
3. Emplégase'l teorema fundamental del cálculu, suponiendo que nin l'integrando nin la integral tienen singularidaes nel camín d'integración, #:

$\int _{a}^{b}f(x)\,dx=F(b)-F(a).$

1. Poro, el valor de la integral ye F(b) − F(a).

Nótese que la integral nun ye realmente la antiderivada, sinón que'l teorema fundamental dexa emplegar les antiderivadas pa evaluar les integrales definíes.

De cutiu, el pasu difícil d'esti procesu ye'l d'atopar una primitiva de f. En rares ocasiones ye posible echar una güeyada a una función y escribir direutamente la so primitiva. Bien de cutiu, ye necesariu emplegar una de les munches téuniques que se desenvolvieron pa evaluar integrales. La mayoría d'elles tresformen una integral n'otra que s'espera que seya más afechisca. Ente estes téuniques destaquen:

• Integración por cambéu de variable
• Integración por partes
• Integración per sustitución trigonométrica
• Integración de fracciones parciales

Inclusive si estes téuniques fallen, entá pue ser posible evaluar una integral dada. La siguiente téunica más común ye'l cálculu de la residuu, ente que la serie de Taylor dacuando puede usase pa topar la primitiva de les integrales non elementales no que se conoz como'l métodu d'integración por series. Tamién hai munches formes menos habituales pa calcular integrales definíes; por casu, puede emplegase la identidá de Parseval pa tresformar una integral sobre una rexón rectangular nuna suma infinita. En delles ocasiones, puede evaluase una integral emplegando un trucu; un exemplu d'esti tipu puede vese na integral de Gauss.

Los cálculos de volumes de sólidu de revolución sólidos de revolución pueden faese de normal cola integración por discos o la integración por capes.

Los resultaos específiques que s'atoparon emplegando les distintes téuniques recoyer na tabla d'integrales.

Algoritmos simbólicos

Artículu principal: Integración simbólica

En munchos problemes de matemátiques, física, ya inxeniería nos que participa la integración ye deseable tener una fórmula esplícita pa la integral. Con esta finalidá, a lo llargo de los años fuéronse publicando estenses tables d'integrales. Col desenvolvimientu de los ordenadores, munchos profesionales, educadores y estudiantes recurrieron a los sistemes de cálculu alxebraicu por ordenador, que fueron diseñaos específicamente pa desenvolver xeres aburribles o difíciles, ente les cualos atópase la integración. La integración simbólica presenta un retu especial nel desenvolvimientu d'esti tipu de sistemes.

Una dificultá matemática importante de la integración simbólica ye que, en munchos casos, nun esiste nenguna fórmula zarrada pa la primitiva d'una función aparentemente inocente. Por casu, sábese que les primitives de les funciones exp (x²), x^x y sen x /x non pueden espresase con una fórmula zarrada nes que participen solu funciones racionales, esponenciales, logarítmiques, trigonométriques, inverses de les funciones trigonométriques, y les operaciones de suma, multiplicación y composición. N'otres pallabres, nenguna d'estos trés funciones daes ye integrable con funciones elementales. La teoría de Galois diferencial apurre criterios xenerales pa determinar cuándo la primitiva d'una función elemental ye de la mesma elemental. Por desgracia, resulta que les funciones con espresiones zarraes pa les sos primitives son la esceición en cuenta de ser la regla. Arriendes d'ello, los sistemes de cálculu alxebraicu por ordenador, nun pueden tener la seguridá de poder atopar una primitiva pa una función elemental cualesquier construyida de forma aleatoria. Nel llau positivu, si afítense de mano los "bloques constructivos" de les primitives, entá ye posible decidir si puede espresase la primitiva d'una función dada emplegando estos bloques y les operaciones de multiplicación y composición, y topar la respuesta simbólica nel casu de qu'esista. El algoritmu de Risch, implementáu en Mathematica y n'otros sistemes de cálculu alxebraicu por ordenador, faen precisamente esto pa funciones y primitives construyíes a partir de fracciones racionales, raigañu d'una función radicales, llogaritmos y funciones esponenciales.

Dellos integrandos apaecen cola abonda frecuencia como pa merecer un estudiu especial. En particular, pue ser útil tener, nel conxuntu de les primitives, les funciones especiales de la física (como les funciones de Legendre, la función hipergeométrica, la función gamma, etcétera). Ye posible estender l'algoritmu de Risch-Norman de forma que tome estes funciones, pero trátase de too un retu.

La mayoría de los humanos nun son capaces d'integrar estes fórmules xenerales, polo que per un sitiu los ordenadores son más hábiles integrando fórmules bien complicaes. Ye pocu probable que les fórmules bien complexes tengan primitives de forma zarrada, de cuenta qu'hasta qué puntu esto ye una ventaya ye una cuestión filosófica abierta a alderique.

Cuadradura numbérica

Métodos numbéricos de cuadradura: ■ Rectángulu, ■ Trapezoide, ■ Romberg, ■ Gauss.

Artículu principal: Integración numbérica

Les integrales que s'atopen nos cursos básicos de cálculu fueron escoyíes deliberadamente pola so simplicidá, pero les que s'atopen nes aplicaciones reales non siempres son tan algamadices. Delles integrales non pueden topase con exactitú, otres precisen de funciones especiales que son bien complicaes de calcular, y otres son tan complexes qu'atopar la respuesta exacta ye demasiáu lentu. Esto motiva l'estudiu y l'aplicación de métodos numbéricos p'averar integrales. Anguaño úsense na aritmética de coma flotante, en ordenadores electrónicos. Pa los cálculos a mano surdieron munches idees muncho primero; pero la velocidá de los ordenadores d'usu xeneral como'l ENIAC crearon la necesidá de meyores.

Los oxetivos de la integración numbérica son la exactitú, la fiabilidá, la eficiencia y la xeneralidá. Por casu, la integral

$\int _{-2}^{2}{\tfrac {1}{5}}\left({\tfrac {1}{100}}(322+3x(98+x(37+x))-24{\frac {x}{1+x^{2}}}\right)dx$

que tien el valor averáu de 6.826 (na práutica ordinaria nun se conoz de mano la respuesta, polo qu'una xera importante — que nun s'esquiza equí — ye decidir en qué momentu un aproximamientu yá ye bastante bona.) Un enfoque de "llibru de cálculu" estrema l'intervalu d'integración en, por casu, 16 cachos iguales, y calcula los valores de la función.

Valores de la función nos puntos

x	−2,00		−1,50		−1,00		−0,50		0,00		0,50		1,00		1,50		2,00
f(x)	2,22800		2,45663		2,67200		2,32475		0,64400		−0,92575		−0,94000		−0,16963		0,83600
x		−1.75		−1,25		−0,75		−0,25		0,25		0,75		1,25		1.75
f(x)		2,33041		2,58562		2,62934		1,64019		−0,32444		−1,09159		−0,60387		0,31734

Delles aplicaciones

Valor mediu d'una función

Pa calcular el valor mediu m d'una función f nun intervalu [a,b] úsase la siguiente fórmula:

$m={\frac {1}{b-a}}\int _{a}^{b}f(x)\mathrm {d} x.$

Nótese que, si la función f ye una función gradiada con pasos d'igual anchor, esta definición coincide cola media aritmética de los valores de la función. Si los pasos tienen anchores distintos, entós coincide cola media aritmética ponderada onde'l valor de la función en cada pasu sopesar col anchor del pasu. Poro, esta definición puede entendese como la estensión natural de la media.

Aplicaciones en física

Munches lleis de la Física espresar en forma d'ecuaciones diferenciales. Nel casu más senciellu, estes ecuaciones diferenciales resolver col cálculu d'una primitiva y munches vegaes la resultancia final que se busca atopar col cálculu d'una integral.

Por casu, la integral aplicar pa resolver el problema de la cayida llibre d'un cuerpu sometíu a la gravedá de la tierra. Na Tierra, l'aceleración de la gravedá ye aproximao g = 9,81 m/s². Polo tanto un cuerpu que cai llibremente empezando la so cayida con velocidá nula tien una velocidá que vien dada pola siguiente función:

$v=-g\cdot t$

El signu negativu ye por cuenta de que la gravedá ye escontra'l centru de la tierra y los sistemes de referencia de normal escuéyense de forma que la direición positiva ye escontra riba.

Si quier sabese la distancia que percorrió'l cuerpu mientres un tiempu dau T puede razonase (emplegando analís non estándar) qu'en redol a cada poco t la velocidá ye constante salvu variaciones infinitesimales, polo tanto l'espaciu percorríu nesti intre mientres un periodu de tiempu infinitesimal dt ye v(t)dt, la suma de tolos espacios percorríos mientres tolos intres dende t=0 hasta t=T (el momentu en que quier sabese la distancia percorrida) y calcúlase cola integral:

$\ell =\int _{0}^{T}\left(-g\cdot t\;\mathrm {d} t\,\right)$.

La resultancia d'esta integral ye:

$\ell =\,-({\frac {g}{2}}\cdot T^{2})$

Otros exemplos de campos de la física onde s'apliquen les integrales:

• La enerxía consumida nun periodu de tiempu ye la integral de la potencia mientres el tiempu.
• La variación de la carga llétrica nun condensador mientres un periodu de tiempu ye la integral de la corriente llétrica que flúi escontra'l condensador mientres esti tiempu.
• La integración del caudal (metros cúbicos per segundu) que flúi por un conductu apurre'l volume de fluyíu que pasó pol conductu mientres el periodu d'integración.

Ver tamién

• Tabla d'integrales
• Integración numbérica
• Derivada
• Signu d'Integral

• Sumatorio
• Llende matemática
• Infinitu
• Integral de llinia
• Cambéu de variable
• Integrales definíes
• Integrales indefiníes

Bibliografía

• Apostol, Tom M. (1967). Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra, 2nd, John Wiley & Sons. ISBN 978-0-471-00005-1.
• Bourbaki, Nicolas (2004). Integration I. Springer. ISBN 3-540-41129-1.. En particular los capítulos III y IV.
• Burton, David M. (2005). The History of Mathematics: An Introduction, 6th, McGraw-Hill, páx.  359. ISBN 978-0-07-305189-5.
• Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing, páx. 247-252. ISBN 978-0-486-67766-8.
• Dahlquist, Germund; Björck, Åke (forthcoming) «Chapter 5: Numerical Integration», Numerical Methods in Scientific Computing. Philadelphia: SIAM.
• Folland, Gerald B. (1984). Real Analysis: Modern Techniques and Their Applications, 1st, Wiley-Interscience. ISBN 978-0-471-80958-6.
• Fourier, Jean Baptiste Joseph (1822). Théorie analytique de la chaleur. Chez Firmin Didot, père et fils, páx. §231.
  Disponible n'inglés comoFourier, Joseph (1878). The analytical theory of heat, Freeman, Alexander (trans.), Cambridge University Press, páx. 200-201.
• (2002) The Works of Archimedes. Dover. ISBN 978-0-486-42084-4.
  (Orixinalmente publicáu por Cambridge University Press, 1897, based on J. L. Heiberg's Greek version.)
• Hildebrandt, T. H. (1953). Integration in abstract spaces 59, páx. 111-139.
• Kahaner, David; Moler, Cleve; Nash, Stephen (1989) «Chapter 5: Numerical Quadrature», Numerical Methods and Software. Prentice-Hall. ISBN 978-0-13-627258-8.
• Leibniz, Gottfried Wilhelm (1899). Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band. Berlin: Mayer & Müller.
• Miller, Jeff. Earliest Uses of Symbols of Calculus. Consultáu'l 2 de xunu de 2007.
• O'Connor, J. J.; Robertson, Y. F. (1996) A history of the calculus. Consultáu'l 9 de xunetu de 2007.
• Rudin, Walter (1987). «Chapter 1: Abstract Integration», Real and Complex Analysis, International, McGraw-Hill. ISBN 978-0-07-100276-9.
• Saks, Stanisław (1964). Theory of the integral, English translation by L. C. Young. With two additional notes by Stefan Banach. Second revised, New York: Dover.
• Stoer, Josef; Bulirsch, Roland (2002) «Chapter 3: Topics in Integration», Introduction to Numerical Analysis, 3rd, Springer-Verlag. ISBN 978-0-387-95452-3..
• W3C (2006). Arabic mathematical notation.

Llibros n'internet

• Keisler, H. Jerome, Elementary Calculus: An Approach Using Infinitesimals, University of Wisconsin
• Stroyan, K.D., A Brief Introduction to Infinitesimal Calculus, University of Iowa
• Mauch, Sean, Sean's Applied Math Book, CIT, an online textbook that includes a complete introduction to calculus
• Crowell, Benjamin, Calculus, Fullerton College, an online textbook
• Garrett, Paul, Notes on First-Year Calculus
• Hussain, Faraz, Understanding Calculus, an online textbook
• Kowalk, W.P., Integration Theory Archiváu 2012-02-27 en Wayback Machine, University of Oldenburg. A new concept to an old problem. Online textbook
• Sloughter, Dan, Difference Equations to Differential Equations, an introduction to calculus
• Numerical Methods of Integration at Holistic Numerical Methods Institute

Enllaces esternos

• Wikillibros tien un llibru o manual sobre Cálculu. (n'inglés)
• integral definida_y_la_funcion_area/sumariu.html La integral definida y la función área, en Descartes.
• The Integrator de Wolfram Research
• Function Calculator de WIMS
• Wang, P. S. Evaluation of Definite Integrals by Symbolic Manipulation (1972) - a cookbook of definite integral techniques

• Datos: Q80091
• Multimedia: Integration (mathematics)